первый перепишем уравнение в виде
x^2-(a+1)x+a=0
по теореме Виета , имеем:
(x1)+(x2)=a+1
(x1)(x2)=a
(x1)^2+(x2)^2=(x1+x2)^2-2(x1)(x2)=(a+1)^2-2a=a^2+2a+1-2a=a^2+1
ответ: a^2+1
второй разложим на множители
x(x-a)-1(x-a)=0
(x-1)(x-a)=0
октуда видно что один корень даного уравнения равен 1, второй равен а
значит сумма квадратов корней данного уравнения равна 1^2+a^2=a^2+1
овтет: a^2+1
(можно как вариант еще:
найти корни через дискриминант, а потом опять таки зная корни посчитать сумму их квадратов)
садовый участок прямоугольной формы площадью 600 м2 обнесён забором, длина которого 100м. Чему равны стороны участка? Чему равны стороны участка такой же площади, если длина забора вокруг него составляет 140м?
Примем
периметр (длина забора) первого участка Р1=100 м
периметр (длина забора) второго участка Р2=140 м
длина первого участка - а1
ширина первого участка - в1
длина второго участка - а2
ширина второго участка - в2
Тогда
(а1+в1)*2=100
(а2*+в2)*2=140
а1*в1=а2*в2=600
а1+в1=50
а1=50-в1
подставляем
а1*в1=600
(50-в1)*в1=600
50*в1-(в1)^2=600
или
-(в1)^2+50*в1-600=0
Решаем с дискриминантом
D=b^2-4*а*с=50^2-4*(-1)*(-600)=100
(В1)1=[(-b-D^(1/2))/2*a=[-50-100^(1/2)]/2*(-1)=(-50-10)/(-2)=30
(В1)2=[(-b+D^(1/2))/2*a=[-50+100^(1/2)]/2*(-1)=(-50+10)/(-2)=20
т.е. ширина первого участка может быть: 30 и 20 м
(а1)1=50-в1=50-30=20 м
(а1)2=50-в1=50-20=30 м
То есть первый участок размерами 20 на 30 м
аналогично решаем и второй участок
а2*в2=600
(а2+в2)*2=140
а2=70-в2
подставляем
а2*в2=600
(70-в2)*в2=600
70*в2-(в2)^2=600
или
-(в2)^2+70*в2-600=0
Решаем с дискриминантом
D=b^2-4*а*с=70^2-4*(-1)*(-600)=2500
(В2)1=[(-b-D^(1/2))/2*a=[-70-2500^(1/2)]/2*(-1)=(-70-50)/(-2)=60
(В2)2=[(-b+D^(1/2))/2*a=[-70+2500^(1/2)]/2*(-1)=(-70+50)/(-2)=10
т.е. ширина второго участка может быть: 60 и 10 м
(а2)1=70-в2=70-60=10 м
(а2)2=70-в2=70-10=60 м
То есть второй участок размерами 10 на 60 м
Проверим:
Периметр второго участка Р2=(10+60)*2=140
140=140
Площадь второго участка = 10*60=600 м^2
600 м^2=600 м^2
Стороны второго участка равны 10 и 60 м
см. рисунок
если MO - радиус, то ME диаметр, где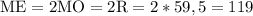
Тогда, в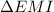 :
:
ответ: 105