Question

На каком множестве функция F(x)=3/x-2 не является первообразной для функции f(x)=-3/(x-2)^2. С решением

Answer 1

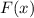Функция $F(x)$ дифференцируема во всех точках, кроме точки $x=2$ (ведь знаменатель обращается в ноль).

Найдём производную функции по правилу производной частного:

$F'(x)=\dfrac{3' \cdot (x-2)-(x-2)' \cdot 3}{(x-2)^2}=\dfrac{0-1}{(x-2)^2}=-\dfrac{1}{(x-2)^2}$

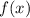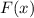Это мы проверили, правильно ли записана задача. Обе функции, $f(x)$ и $F(x)$ определены на 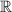$\mathbb R$, кроме точки $x=2$.

ответ: C)