ответ: 52л; 59л
Объяснение:
Пусть х (л) кваса будет во второй ёмкости, тогда х+7 (л) – в первой. Составим уравнение:
1. Запишем по две стороны от равно первую ёмкость х и вторую х+7. Из первой перельём (то есть вычтем) 15 литров и добавим их (приплюсуем) ко второй. Знаем, что во второй в 2 раза больше литров кваса после того, как мы перелили. Значит, чтобы в первой было столько же, сколько во второй, нужно умножить на 2. Пишем уравнение:
2(х - 15) = (х + 7) + 15
2х - 30 = х + 7 + 15
2х - х = 7 + 15 + 30
х = 52 (л) – в первой ёмкости
х + 7 = 52 + 7 = 59 (л) – во второй ёмкости
ответ: 52л; 59л
В решении.
Объяснение:
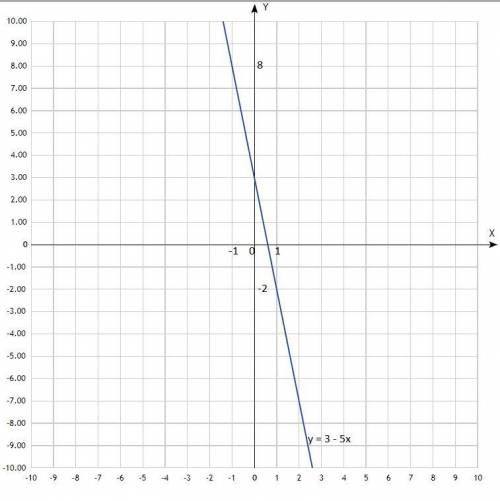
1) Постройте график функции у = 3 - 5х.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 3 - 5х
Таблица:
х -1 0 1
у 8 3 -2
По вычисленным точкам построить прямую.
2) Проходит ли график функции у = -5х + 4 через точку М(-7; 39)?
Нужно подставить известные значения х и у (координаты точки) в уравнение. Если левая часть равна правой, то проходит, и наоборот.
у = -5х + 4; М(-7; 39);
39 = -5*(-7) + 4
39 = 39, проходит.
3) Дана функция у = 1/4 х - 8. Найти значение функции, если значение аргумента равно 12.
Проще, найти значение у, если х = 12.
Подставить значение х в уравнение и вычислить у:
у = х/4 - 8
у = 12/4 - 8
у = 3 - 8
у = -5;
При х = 12 у = -5.
? - 17%
(1755*17):100=298,35
1755-298,35=1456,65
ответ: 1456,65