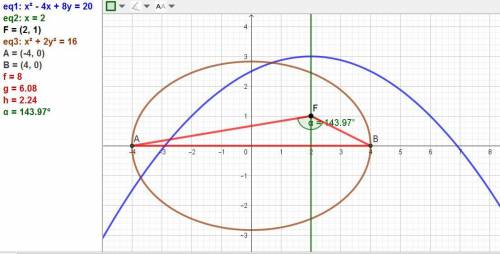
Даны парабола x²-4x+8y-20=0 и эллипс x²+2y²=16.
Приведём их к каноническому виду.
Парабола (x²-4x+4)-4+8y-20=0, (x - 2)² = -8y + 24.
Получаем (x - 2)² = 2*(-4)*(y - 3) уравнение параболы с осью х = 2, параметром р = -4 и вершиной в точке (2; 3)
Тогда фокус будет в точке F(2; 3-(4/2)) = (2; 1).
Эллипс x²+2y²=16, (x²/4²)+(y²/(√8)²)=1.
Его большая ось от х = -4 до х = 4.
Это точки А(-4; 0) и В(4; 0).
Находим векторы: FA = (-6; -1), |FA| = √37.
FB = (2; -1), |FB| = √5.
cos F = (-6*2 + (-1)*(-1)/(√37*√5) = -11/√185 ≈ -0,808736084.
F = 2,512796367 радиан.
F = 143,9726266 градусов.
1) -41; 2) -20
Объяснение:
f(x) = -2x²+5x-8
1) f(-3) = -2(-3)²+5(-3)-8 = -2*9-15-8 = -18-23 = -41
2) f(4) = -2*4²+5*4-8 = -2*16+20-8 = -32+12 = -20