Метод матем индукции 1) проверим делимость на 3 при n=1 при n=1 4n^3+6n^2+5n+9=4+6+5+9=24 - делится на 3 2) предположим что делится на 3 при n=k при n=к 4n^3+6n^2+5n+9=4k^3+6k^2+5k+9=(3k^3+6k^2+3k+9)+(k^3+2k) - делится на 3 значит (k^3+2k) - делится на 3, так как (3k^3+6k^2+3k+9) делится на 3 3) проверим делимость на 3 при n=k+1 при n=к+1 4n^3+6n^2+5n+9=4(к+1)^3+6(к+1)^2+5(к+1)+9= =(3(к+1)^3+6(к+1)^2+3(к+1)+9)+((к+1)^3+2(к+1)) = A+B A=(3(к+1)^3+6(к+1)^2+3(к+1)+9) - делится на 3 B=(к+1)^3+2(к+1)=k^3+3k^2+3k+1+2k+2=(k^3+2k)+(3k^2+3k+3) = C+D C = (k^3+2k) - делится на 3 (см пункт 2) ) D = (3k^2+3k+3) - делится на 3 значит B=C+D - делится на 3 значит 4n^3+6n^2+5n+9 при n=k+1 делится на 3 так как n=k+1 4n^3+6n^2+5n+9 = A+B <<< доказано методом математической индукции >>>>
Комментарий не учитывать, - условие правильное...)))
Дано: t = 6 ч Решение: S = 36 км Обозначим х км/ч - скорость лодки S₁ = 2 км у км/ч - скорость течения реки S₂ = 6 км Получаем систему: t₁ = t₂ ------------------------------ Найти: Производим замену: а = х + у b = х - у Тогда: 36а + 36b = 6аb а = 3b (подставляем в первое) => 36*3b + 36b = 18b² 144b = 18b² b = 8 и a = 3b = 24 24 = x + y 24 = 2y + 8 y = 8 8 = x - y x = y + 8 x = 16
ответ: скорость течения реки 8 км/ч, скорость лодки 16 км/ч --------------------------------------------------------------------------------------------------- Можно еще проще решить..))
Условие то же. Решение: Обозначим х - скорость лодки, у - скорость течения реки Тогда: 2(х + у) = 6(х - у) 8у = 4х х = 2у (1) 36/(x+y) + 36/(x-y) = 6 - подставляем из (1) 36/3y + 36/y = 6 48/y = 6 y = 8 х = 16
ответ: скорость течения реки 8 км/ч, скорость лодки 16 км/ч
Производим замену: а = х + у 
2сos x = -1
cos x =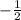
x = ± arccos x + 2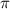
n , n ∈ Z
x = ±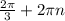
, n ∈ Z
Відповідь: ±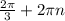
, n ∈ Z. (Б)