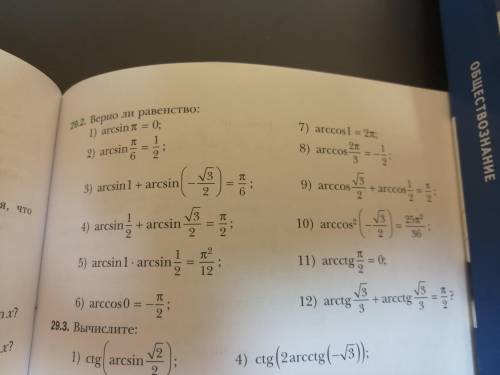
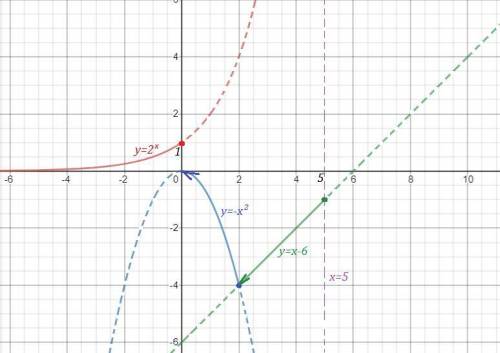
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
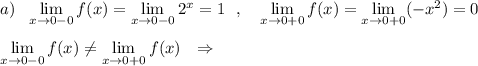
При х=0 функция имеет разрыв 1 рода .
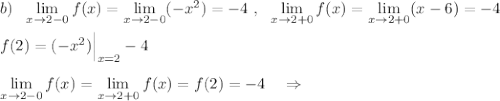
При х=2 функция непрерывна.
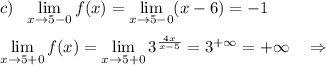
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
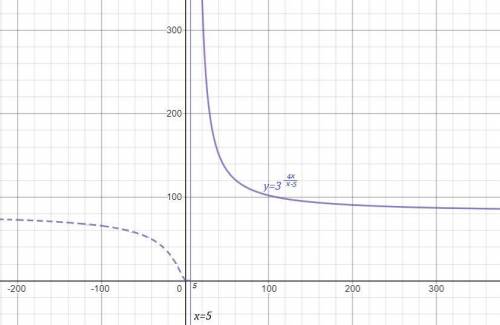
На 1 рисунке нет чертежа функции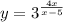 
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
y= -x² + 4x - 3
Объяснение:
Построить график функции, это парабола cо смещённым центром, ветви параболы направлены вниз.
а)найти координаты вершины параболы:
х₀ = -b/2a = -4/-2 = 2
y₀ = -(2)²+4*2-3 = -4+8-3 = 1
Координаты вершины (2; 1)
б)Ось симметрии = -b/2a X = -4/-2 = 2
в)найти точки пересечения параболы с осью Х, нули функции:
y= -x²+ 4x - 3
-x²+ 4x - 3=0
x²- 4x + 3=0, квадратное уравнение, ищем корни:
х₁,₂ = (4±√16-12)/2
х₁,₂ = (4±√4)/2
х₁,₂ = (4±2)/2
х₁ = 1
х₂ = 3
Координаты нулей функции (1; 0) (3; 0)
г)Найти точки пересечения графика функции с осью ОУ.
Нужно придать х значение 0: у= -0+0-3=-3
Также такой точкой является свободный член уравнения c, = -3
Координата точки пересечения (0; -3)
д)для построения графика нужно найти ещё несколько
дополнительных точек:
х=-1 у= -8 (-1; -8)
х= 0 у= -3 (0; -3)
х=4 у= -3 (4;-3)
х= 5 у= -8 (5;-8)
Координаты вершины параболы (2; 1)
Координаты точек пересечения параболы с осью Х: (1; 0) (3; 0)
Координаты дополнительных точек: (-1; -8) (0; -3) (4;-3) (5;-8)
e)В первой, третьей и четвёртой четвертях.