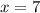
Объяснение:
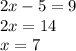
Периодическая десятичная дробь - это любая десятичная дробь, у которой:
1) Значащая часть состоит из бесконечного количества цифр;
2) Через определенные интервалы цифры в значащей части повторяются.
вот такой набор из повторяющихся цифр - называется периодической частью дроби
а теперь попробуем выполнить задание
1) 3/11=
Просто делим число 3 на 11
3/11=0,2727272727...
мы видим что повторяются цифры 27,
Значит нашу дробь мы записываем так: 3/11=0,(27)
2) 95/335=0,2835820895522388...
Мы видим что нет повторяющихся цифр
Значит эта дробь не периодическая
3) 35/111=0,315315315315..
повторяются цифры 315, Значит запись будет выглядеть так
35/111=0,(315)
4) 13/15= 0,8666666...
повторяется цифра 6, значит записывает так:
13/15=0,8(6)
5) 7/12=0,583333333...
Значит записываем так
7/12=0,58(3)
представим бесконечную периодическую десятичную дробь в виде суммы:
0,(3)=0,3+0,03+0,003+... .
В правой части слагаемые геометрической прогрессии у которой первый член равен 0,3, а знаменатель 0,1, т.е. q<1, значит имеем бесконечную геометрическую прогрессию. Находим сумму этой прогрессии:
S=0,3/(1-0,1)=0,3/0,9=3/9=1/3, значит 0,(3)=1/3 и все по аналогии.
Если например бесконечная дробь периодическая где сотые и тысячные, то сумма соответственно будет состоять из сотых и тысячных, т.е.:
наприер:0,(17)=0,17+0,0017+0,000017+... .
2х-5=9
2х=9+5
2х=14 |:2
х=7