Чтобы обратить периодическую дробь в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и записать эту разность числителем;
в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после девяток дописать столько нулей, сколько цифр между запятой и первым периодом. Например:
4y2 - 4y + 1 = 0
D = b2 + 4ac = 16 - 16 = 0
x = ( -b +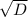 ) / 2a = (4+0) / 8 = 0.5
) / 2a = (4+0) / 8 = 0.5