Выразим данные нам члены прогрессии через седьмой, по определению арифметической прогрессии:
a5 = a7 - 2d, a8 = a7 + d, a10 = a7 + 3d,
тогда уравнение примет вид:
a7 - 2d + a7 + d = a7 + a7 + 3d + 15, =>
=> 2a7 - d = 2a7 + 3d + 15 => -4d = 15 => d = -3, 75
ответ: -3, 75
если 8х-15х^2-1 - это подкоренное выражение, то оно должно быть больше или равно 0.
решаем: -15х^2+8х-1 больше либо равно 0
15х^2-8х+1 меньше либо равно 0 (умножили на -1!)
15х^2-8х+1=0 и находим дискриминант: Д=64-4*15*1=4, значит еорень из Д=2, находим корни х1=(8-2)/2*15=0,2 ; х2=(8+2)/2*15=1/3.
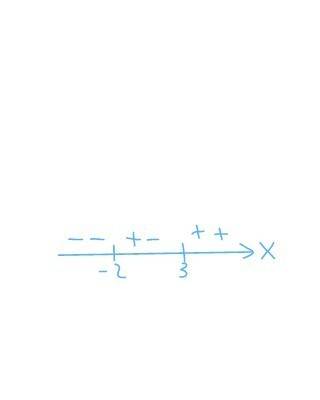
(х-0,2)(х-1/3) меньше либо равно 0.
с промежутков находим: х принадлеж.[0,2;1/3]
значит х может быть равным от 0,2 до 1/3. Область определения функции или ОДЗ - это значения, которые принимает х, и чтобы выражение или неравенство имело смысл
Формула для n-го члена арифметической прогрессии имеет вид:
аn = a₁ + d(n - 1)
Тогда
а₅ = a₁ + 4d
а₈ = a₁ + 7d
Их сумма
а₅ + а₈ = 2a₁ + 11d
а₇ = a₁ + 6d
а₁₀ = a₁ + 9d
Их сумма
а₇ + а₁₀ = 2a₁ + 15d
По условию
а₅ + а₈ - 15 = а₇ + а₁₀
2a₁ + 11d - 15 = 2a₁ + 15d
4d = -15
d = -3,75
ответ: разность арифметической прогрессии d = -3,75