пусть скорость первого авто = х км/ч
S- как половина пути
Первое авто проехал 2S км тогда t=2S/x км/ч
Второй авто первую половину пути (x-10) км/ч тогда t=S/x-10
вторую половину пути 60 км/ч тогда t=S/60
2S/х=S/(х-10)+S/60 домножаем чтобы в знаменателе было одинаково
2*60*(x-10)=1*60x+1*x(x-10)
120x-1200=60x+x^2-10x
-x^2-50x+120x-1200=0
-x^2+70x-1200=0 /*(-1)
x^2-70x+1200=0
D = b2 - 4ac
D = 4900 - 4800 = 100 = 10^2
x1,2 = -b ± √D/2a
x1 = 70 + 10/2 = 80/2 = 40 (больше 39 )
x2 = 70 - 10/2 = 60/2 = 30(не удол.)
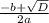 =
= 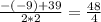 = 12
= 12 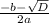 =
=  = -7,5 - не подходит, потому что х<0
= -7,5 - не подходит, потому что х<0 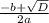 =
= 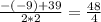 = 12
= 12 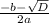 =
=  = -7,5 - не подходит, потому что х<0
= -7,5 - не подходит, потому что х<0
Пусть х км/ч - скорость первого автомобиля, а S - расстояние от А до В, тогда время в пути первого автомобиля равно S/х часов. Второй автомобиль первую половину пути ехал со скоростью (х-10) км/ч и потратил на это S/2(х-10) часов, на вторую половину пути он затратил S/(2*60)=S/120 часов. Весь путь был пройден автомобилями за S/х или S/2(х-10)+S/120 часов. Составим и решим уравнение:
S/х=S/2(х-10)+S/120 |*120x(x-10)/S (из условия ясно, что S>0)
120(x-10)=60x+x(x-10)
120x-1200=60x+x^2-10x
x^2+50x-120x+1200=0
x^2-70x+1200=0
по теореме Виета:
x1=40 x2=30<39 (не удовлетворяет условию)
ответ: скорость первого автомобиля 40 километров в час.