Question

Решать всё не нужно просто абъесните как решать на 1 примере. Просто тему не понял ;(​

Answer 1

$3x^2+10x-8\geq 0$

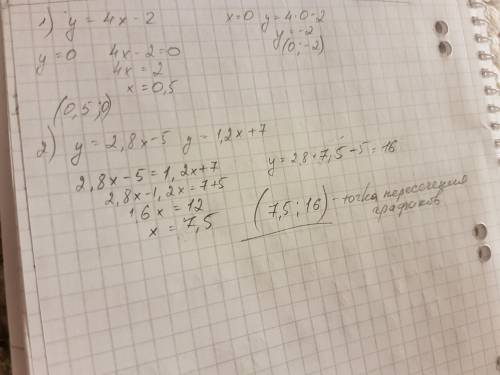
Находим корни уравнения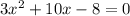  $3x^2+10x-8=0$  .

$D/4=5^2-3\cdot (-8)=49\ \ ,\ \ \ x_{1,2}=\dfrac{-5\pm 7}{3}\ \ ,\ \ \ x_1=-4\ ,\ x_2=\dfrac{2}{3}$

Дальше можно : либо методом интервалов, либо начертив параболу (схематично) .

1)  Метод интервалов.

Раскладываем квадратный трёхчлен на множители.

$3x^2+10x-8=3(x-x_1)(x-x_2)=3(x+4)(x-\frac{2}{3})\\\\3(x+4)(x-\frac{2}{3})\geq 0$

На числовой оси отмечаем нули функции (то есть корни кв. трёхчлена) . Вычисляем знаки на каждом интервале. Нас интересует знак (+), так как знак неравенства  " ≥ " .

Знаки:     $+++[-4\ ]---[\ \frac{2}{3}\ ]+++$

ответ:    $x\in (-\infty \, ;-4\ ]\cup [\ \frac{2}{3}\ ;+\infty \, )$

2)   Начертим схематично параболу, учитывая, что ветви её направлены вверх, так как коэффициент при  х²  равен 3>0 .

И посмотрим, на каких промежутках график лежит выше оси ОХ .

В обоих случаях учитываем , что знак неравенства не строгий, а поэтому корни (нули функции) входят в нужные промежутки .

См. рисунок.

ответ:  $x\in (-\infty \, ;-4\ ]\cup [\ \frac{2}{3}\ ;+\infty \, )$  .