37.2. Найдите значение выражения: 2х - 1
1)
при х = 3; 1; -5; -1,6; 100;
2)
За 7
2а + 5
при а= -2; – 0,4; 0; 2,5;
3)
6² +6
3b - 4
при b = 3; 4,4; 5; 6;
1
8
4) 2x +
при х =
x + 1
0,5; 1; 3;
2
у + 3
2 у
5)
+
при у = 1,5; 2,5; 4; 4,5;
2 у
у - 3
x + 3
6)
+
х
при х = --
; 1,5; 2; 3;
3
2
7)
(a + b) - 1
a²+1
2a-b
при а=-3, b = -1;
8)
при а = 1, b = 0,5.
1
а
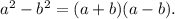
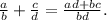
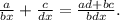
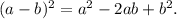
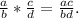

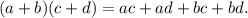
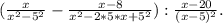
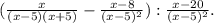
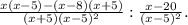
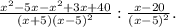
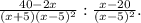
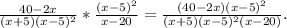
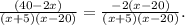
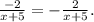
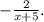
1. Разность квадратов.
2. Приведение дробей к общему знаменателю.
Причем, если знаменатели имеют общий множитель, то на него можно и не домножать. Как к примеру тут:
3. Квадрат разности.
4. Умножение дробей.
(Числитель умножаем с числителем, а знаменатель - со знаменателем.)
5. Деление дробей.
(Вторую дробь (делитель) переворачиваем, а знак деления заменяем умножением.)
6. Умножение многочлена на многочлен.
Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена.
1). Преобразуем немного наше выражение.
2). Видно, что в знаменателе первой дроби можно использовать формулу разности квадратов, а в знаменателе второй дроби полный квадрат (квадрат разности). Применим эти формулы.
3). Приведем первые две дроби общему знаменателю.
4). Раскрываем скобки в числителе первой дроби.
5). Приводим подобные слагаемые.
6). Делим, а затем умножаем дроби.
7). Сокращаем дроби и выносим общий множитель (-2) в числителе.
8). Опять сокращаем.
ответ: