Объяснение:
1
(x-1)^2-(x+3)(x-3)=x^2-2x+1-(x^2-9)=
=x^2-2x+1-x^2+9= - 2x+10
2
(a+1)(a-1)(a^2+1)-(9+a^2)^2=
=(a^2-1)(a^2+1)-(81+18a^2+a^4=
a^4-1-81-18a^2-a^4=
= - 18a^2-82
a=1/3
-18×(1/3)^2-82= - 18×1/9-82=
= - 2-82= - 84
3
(2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)^2+6y
6y^2+2y-9y-3+2(y^2-25)=2(1-4y+4y^2)+
+6y=
=6y^2+2y-9y-3+2y^2-50=2-8y+8y^2+6y=
=8y^2-7y-53-8y^2+2y=2
-5y=2+53
-5y=55
y= - 11
В решении.
Объяснение:
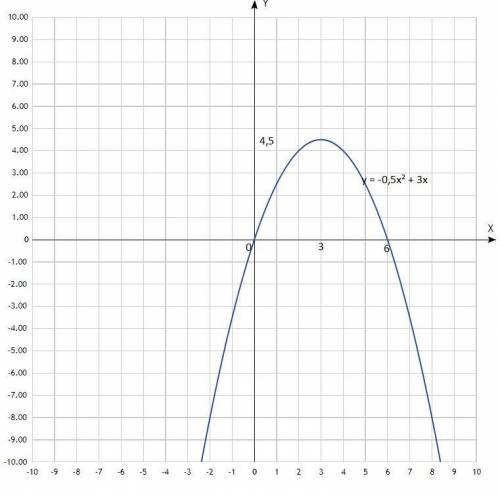
Дана функция у = -1/2 х² + 3х; найти промежуток её убывания.
Построить график функции.
Сначала преобразовать уравнение функции для упрощения.
-1/2 х² + 3х = -0,5х² + 3х, неполное квадратное уравнение.
Приравнять к нулю:
-0,5х² + 3х = 0
0,5х (-х + 6) = 0
0,5х = 0;
х₁ = 0;
-х + 6 = 0
-х = -6
х = 6;
График - парабола, ветви направлены вниз, пересекают ось Ох в точках: х = 0; х = 6 (нули функции).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2 4 6 8
у -8 -3,5 0 2,5 4 4 0 -8
По вычисленным точкам построить параболу.
Согласно графика, функция убывает в промежутке х∈(3; +∞).
1) (x-1)(2)-(x+3)(x-3)=x^2 - 2x + 1 - (x^2 - 9) = x^2-2x+1-x^2 + 9 = -2x + 10
2) (а+1)(а-1)(а²+1)-(9+а²)² = (a²-1)(a²+1) - (9+a²)² = a⁴ -1 - 81 - 18a² - a⁴ = -18a² - 82= -18(1/3)² - 82 = -2 - 82 = -84
3) (2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)²+6y
6y^2+2y-9y-3+2(y^2+5y-5y-25)=2(1-4y+4y^2)+6y
6y^2-7y-3+2y^2-50=2-8y+8y^2+6y
8y^2-8y^2-55=5y
-55=5y
y=-11