Объяснение:
7)4-2m+m^2
8)100+20c+c^2
9)25-10y+y^2
10)36+12n+n^2
11)49-14t+t^2
12)121+22k+k^2
13)1+4d+4d^2
14)25-30y+9y^2
15)64+80y+25y^2
16)16-56n+49n^2
17)4+32c+64c^2
18)9-72q+144q^2
19)16a^2+24a+9
20)25y^2-80y+64
21)4d^2+24d+36
22)81m^2-18m+1
23)49n^2+28n+4
24)64p^2-64p+16
-3.
Объяснение:
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.
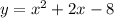
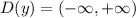
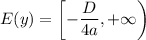- где D дискриминант.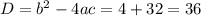
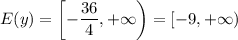
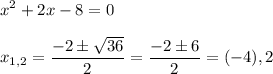
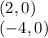
![(-\infty,-1]](/tpl/images/0467/5865/91666.png)
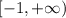
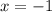
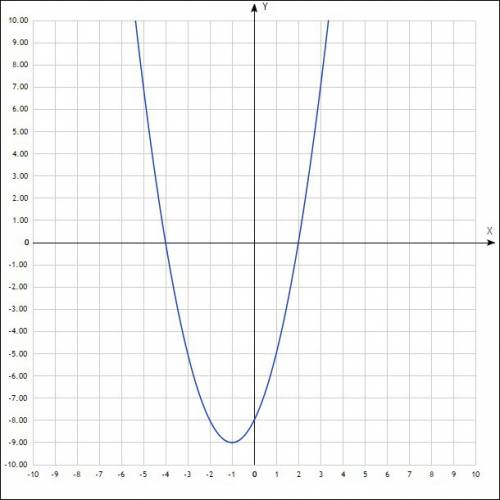
Объяснение:
ответы на уравнения представлены на фотографии