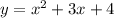
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
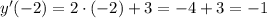
Уравнение касательной имеет вид:
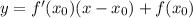
Подставим значение 
Итак, уравнение касательной заданной функции: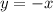 
Воспользуемся геометрическим смыслом касательной: коэффициент наклона 
касательной 
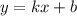численно равен тангенсу угла наклона 
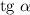с положительным направлением оси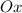 
В найденной касательной коэффициент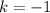 
, следовательно, 
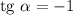при 
или 
ответ: или
1. Сначала требовалось 12 автомашин
2. Фактически использовали 15 автомашин
3. На каждой автомашине планировалось перевозить 5 тонн
Объяснение:
пусть
x - изначальная грузоподъемность одной машины
(т.е. то, сколько тонн груза планировались перевозить на каждой машине изначально)
(x-1) - фактическая грузоподъемность одной машины
(т.е. то, сколько тонн груза фактически перевозили на каждой машине)
y - количество машин, которое требовалось изначально
(y+3) - количество машин, которое потребовалось фактически
по условию: надо перевести 60 тонн,
грузоподъемность × количество машин = масса перевозимого груза
составим систему:
x × y = 60 - изначально
(x-1)×(y+3) = 60 - фактически
решаем систему:
из первого уравнения: x = 60/y
(по условию: y не может быть равен 0)
подставим во второе уравнение:
(60/y - 1) × (y+3) = 60
60 + 180/y - y - 3 = 60
180/y - y - 3 =0
-y^2 -3 × y + 180 = 0
y^2 + 3 × y - 180 = 0
решаем квадратное уравнение:
корни: 12, -15
-15 - отрицательная величина, не подходит по условию
значит
y = 12
тогда
x = 60/12 = 5