v₁ = (-b+√D)/2a = (44+40):6 = 14 (км/ч) v₂ = (-b-√D)/2a = (44-40):6 = 2/3 (км/ч) - не удовлетворяет условию, так как скорость лодки не может быть меньше скорости течения. (чисто математически, если у лодки будет скорость 2/3 км/ч, то она тоже пройдет 8+3=11 км за 45 минут, только последние 3 км она будет двигаться по течению, несмотря на все свои попытки двигаться против..))) Смысла в таком движении точно никакого..))
Пусть Х км/ч- скорость по течению, а У км/ч - скорость против течения 8/Х- время по течению 3/у - время против течения (Х-2) собственная скорость (У+2) собственная скорость 45 мин=45/60 ч =3/4 ч Составим систему уравнений:
{8/Х+3/у=3/4. ⇒ { 8/Х+3/у=3/4 {(Х-2)=(у+2). {Х=у+4 Подставим Х=у+4 в 1-е уравнение : Получим 8/(у+4)+3/у=3/4 Приведём к общему знаменателю, получим: 32у+12у+48=3у²+12у -3у²+32у+48=0 Умножим на (-1) 3у²-32-48=0 Д=√1600=40 У1=(32+40)/6=12 км/ч - скорость против течения У2=(32-40)/6=(-8/6) - не является корнем Х=у+4=12+4=16 км/ч - скорость по течению
диагональ = 20 см
сторона 1 = 12 см
сторона 2= 16 см
Объяснение:
D диагональ
A - одна сторона = D-8
B - вторая сторона = D-4
по теорема Пифагора
C²=A² + B²
C² = (C-8)² + (C-4)² = C² -16C + 64 + C²-8C + 16=2C²-24C + 80
C²-24C + 80 = 0
d=24² - 4*80 = 576-320=256
C1 = (24 +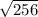
) / 2 = (24+16) / 2 = 40/2 = 20
A=20-8 = 12
B=20-4 = 16
C2 = (24-16) / 2 = 8/2 = 4 (не подходит)
т.к. при С=4 A = 4-8 = -4 (расстояние отрицательным быть не может)