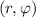Две случайные величины называются независимыми, если закон распределения одной случайной величины не изменяются от того, какие возможные значения приняла другая случайная величина.
Примеры:
1) Бросают два игральных кубика. Здесь количество выпавших очков на одной кубике не влияет от количества очко на другом.
2) В разных цехах изготавливают детали с разным числом бракованных изделий. Количество брака в одном цехе не зависит от количество брака в другом цехе.
3) 2 человека в тире стреляют по разным мишеням. Вероятность попадания каждого по мишеням не зависит от вероятности попадания другого человека.
Корреляционный момент двух независимых случайных величин X иY равен нулю, т.е. для независимых случаяных величин X и Y Kxy=0.
Вычислите при х= -1 значение многочлена х² - 6х - 7.
Упростить ничего нельзя, поэтому просто подставим вместо x -1:
(-1)² - 6 * (-1) - 7
Дальше всё просто: любое число в четной степени положительно, значит (-1)² = 1, это можно доказать: т.к. aⁿ = a * a * a n раз, значит (-1)² -- это -1 * (-1) 2 раза, отсюда -1 * (-1) = 1, поэтому (-1)² = 1.
Отрицательное число, умноженное на отрицательное число, даёт положительное число, значит: -6 * (-1) = 6. Получаем следующее:
(-1)² - 6 * (-1) - 7 = 1 + 6 - 7 = 7 - 7 = 0.
ответ: значение выражения x² - 6x - 7 при x = -1 равно 0.
© Rahmann
Произведём полярную замену![\begin{cases}x=r\cos\varphi\\[2.5pt] y=r\sin\varphi \end{cases}](/tpl/images/1777/9160/c4581.png) с модулем якобиана
с модулем якобиана 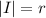
Данная область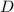 (четверть круга) перейдёт в соответствующую ей область
(четверть круга) перейдёт в соответствующую ей область  в координатах
в координатах