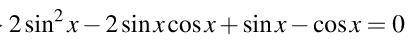
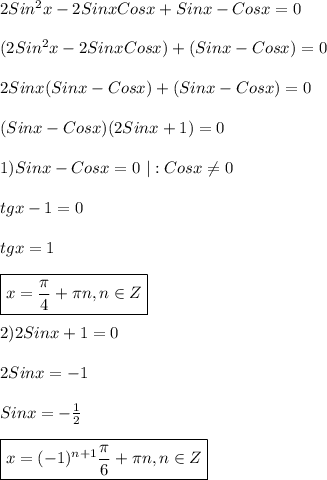
Поделить-то можно, поскольку точки, в которых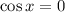 
не являются корнями (при любом из двух значений синуса) данного уравнения, т.е. потери корней не произойдёт.
Но такой ход не оставит уравнения на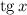 
, поскольку есть синус во второй степени. Даже если поделить на косинус в квадрате -- есть синус в первой степени, который оставит лишний косинус.
x=12, min((16/x)+(x/9))=8/3
Объяснение:
Часть теоремы о средних - неравенство между средним арифметическим и средним геометрическим(неравенство Коши)
(16/x)+(x/9)≥2√((16/x)(x/9))=2√(16/9)=2·4/3=8/3
Равенство достигается при 16/x=x/9⇔x²=144⇔x=±12
x>0⇒x=12
min((16/x)+(x/9))=8/3
Можно решить и другим
Рассмотрим функцию f(x)=16/x+x/9 при x>0. Найдём промежутки её монотонности.
f '(x)=-16/x²+1/9=(x²-144)/(9x²)=(x-12)(x+12)/(9x²)
x∈(0;12)⇒f '(x)<0⇒f↓
x∈(12;+∞)⇒f '(x)>0⇒f↑
minf(x)=f(12)=16/12+12/9=4/3+4/3=8/3
x∈(0;+∞)
(a+3)x^2 = 4a−6x
(a+3)x^2 +6x - 4a = 0
D =b^2 - 4ac = 36 - 4*(-4a)*(a + 3) = 36 + 16a^2 + 48a =
16a^2 + 48a + 36 = 4*(4a^2 + 12a + 9) = 4*((2a)^2 + 2*2a*3 + 3^2) = (2(2a + 3))^2
x12 = (-6 +- |2(2a+3)|)/ 2(a + 3)
x1 = (-6 + 2(2a+3))/ 2(a + 3) = 4a/2(a+3) = 2a/(a+3)
x1 = (-6 - 2(2a+3))/ 2(a + 3) = (-4a - 12)/2(a+3) = -4(a+3)/2(a+3) = -2
D = 0 одно решение
(2(2a + 3))^2 = 0
a = -3/2
x = -6/2(-3/2 + 3) = -6/3 = -2
в других
2 решения (-6 +- 2(2a+3))/ 2(a + 3)
при a = -3 это не квадратное а линейное
линейное уравнение 4a - 6x = -12 - 6x = 0 x = -2
ответ a = -3/2, -3 одно решение , остальные 2 решения
