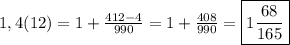
Объяснение:
x=1,4(12) (1)
1) умножаем обе части равенства(1) на 10(10 в степени =количеству знаков после запятой до периода, в нашем случае 1)
10х=14,(12) (2)
2) умножаем обе части равенства (2) на 10 в степени равной кол-ву цифр периода, т.е на 100:
1000х=1412,(12) (3)
3) из (3) вычитаем (2):
1000х-10х=1412,(12)-14,(12)
990х=1412-14
990х=1398
х=1398/990
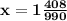
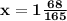
ответ: ymin=y(-4)=-164
Объяснение:
Найдите наименьшее значение функции у = х³ - 5х² + 8х + 12 на отрезке [-4;1].
Найдем значение функции на границах отрезка
у(-4) = (-4)³ - 5·(-4)² +8·(-4) + 12 = -64 - 80 - 32 + 12 = -164
у(1) = 1³ - 5·1² +8·1 + 12 = 1 - 5 + 8 + 12 = 16
Найдем производную функции
у' =(х³ - 5х² + 8х + 12)' = (х³)' - (5х²)' + (8х)' + (12)' = 3x² - 10x +8
Найдем критические точки приравняв производную к нулю
3x² - 10x + 8 = 0
D = (-10)² - 4·3·8 = 100 - 96 = 4
x₁ = (10-2)/(2·3) = 8/6 = 4/3 ≈ 1,33
x₂ = (10+2)/(2·3) = 12/6 = 2
Найденные точки не входят в данный отрезок поэтому значения функции в них находить не будем.
Функция на отрезке монотонна и возрастает. Минимальное значение функции находится в точке x = -4 y(-4) = -164
![РЕШИТЬ.Найдите наименьшее значение функции у=х^3-5х^2+8х+12 на отрезке [-4;1].](/tpl/images/1353/3405/90f6a.jpg)
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f(x) > 0. Алгоритм состоит из 5 шагов:
Решить уравнение f(x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
Найти кратность корней. Если корни четной кратности, то над корнем рисуем петлю. (Корень считается кратным, если существует четное количество одинаковых решений)
Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;
Отметить знаки на остальных интервалах, чередуя их.
После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f(x) > 0, или знаком «−», если неравенство имеет вид f(x) < 0.
В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) =
Объяснение: