a1=0,a2=−0,4,a3=5,9 ответы
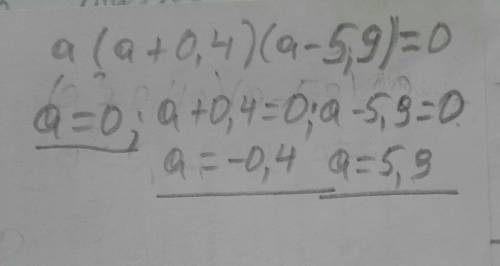
1)sin229° + cos319° + ctg229° * ctg319°=
=sin229°+cos(90°+229°)+ctg(49°+180°)*ctg(139°+180°)
Используя формулу cos(90°+t)=-sint, преобразуем выражение cos(90°+229°)=
=-sin229°
Упростим ctg(49°+180°)=ctg49° и
ctg(139°+180°)=ctg139° ,используя
ctg=(t+k*180°)=ctgt ,где k принадлежит z
В итоге получаем:
sin229°-sin229°+ctg49° * ctg139°=
=ctg49° * ctg139°≈-1
2)( -18cos335°/cos155°*cos60° )-16=
=( -18cos(180°+155°)/cos155°*1/2 )-16=
=( -18cos*(-cos155°)/cos155°*1/2 )-16=
=( -18*-1 / 1*1/2 )-16=( 18/ 1/2 )-16=
=36-16=20
Правильный ответ - это последний
a1=0,a2=−0,4,a3=5,9
Объяснение:
a=0 или a-0,4=0 a=-0,4 или a-5,9=0 a=5,9