Доказальство методом математической индукции.
База индукции n=1 :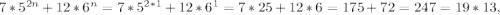 
а значит число выражение 7 * 5 ^ 2n + 12 * 6 ^ n при n=1 делится на 19
Гипотеза индукции. Пусть при n=k выражение 7 * 5 ^ (2n) + 12 * 6 ^ n делится на 19, т.е. выражение 7 * 5 ^ (2k) + 12 * 6 ^ k делится на 19
Инукционный переход. Докажем, что тогда при n=k+1 выражение 7 * 5 ^ (2n) + 12 * 6 ^ n делится на 19
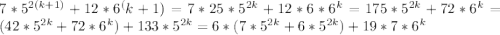, что делится на 19 , так какждый из слагаемых делится на 19 (во второй как в произведение входит множитель 19, в первое слагамое как в произведение по гипотезе индукции входит множитель, который делится на 19)
По принципу математической индукции при любом целом неотрицательном n выражение 7 * 5 ^ 2n + 12 * 6 ^ n делится на 19
=[2·sin((α-3α)/2)·cos((α+3α)/2)/sin2α]·[-2sin(-α)·sin2α/cos2α]=
=[-2·sinα·cos2α/sin2α]·[2sinα·sin2α/cos2α]=
=(-4)·sin²α·(1/2·sin4α)/(1/2·sin4α)=
=-4sin²α;