3) Парабола это квадратичная функция, поэтому ответы: A и B
4) ответы Б и В, т.к
x-2>3
-3x<-12
Переносим числа в правую часть с противоположными знаками: (во втором знак неравенства поменяли, т.к делим на отрицательное x)
x>5
x>4
(От 5 до плюс бесконечности)
5) Арифметическая прогрессия - закономерность, при которой каждый член отличается НА сколько-то.
Значит ответ: -2
Т.к 1-ый член равен 7, а разность -1, мы от 7 должны постепенно отнимать -1, (то, есть 10 раз, 7-1=6-1=5..., пока не дойдём до последнего (10-ого члена прогрессии, а 10-ый член прогрессии это -2))
6) Для начала, нужно решить это квадратное уравнение:
4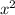
+11x-3=0 (прировняем к нулю)
D=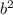
-4ac=121+48=169
x1= -11-13/8= -3
x2= -11+13/8= 0,25
Значит:
4*(x+3)*(x-0,25) (Вот и разложили на трёхчлен)
7)
x+y=3
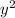-x=39
х=3-у (Это мы выразили x, и нужно подставить его во второе уравнение):
у²-(3-у)-39=0
у²-3+у-39=0
у²+у-42=0
D=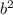-4ac=1²-4·(42)=168+1=169
y₁= -1+13/2=6, y₂= -1-13/2= -7
x₁=3-6=-3
x₂=3-(-7)=3+7=10
ответ:(10;-7) и (-3;6)
8) y=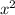-6x+8 (квадратичная функция, значит это парабола)
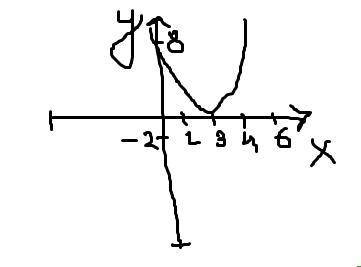
Вершина этой параболы
(3;-1)
Точки пересечение с осями координат:
ax/y=0
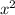-6x+8=0
x1+x2=6
x1*x2=8
(по теореме Виета)
x1=4 (4;0)
x2=2 (2;0)
ay:x=0
y=8 (0;8)
Значит функция убывает при принадлежности x ( -бесконечности до 3 )
Объяснение:
1. Постройте график функции y=2x-1. По графику найдите: а) значения функции при значениях аргумента, равных -2;0;3; б)
значения аргумента, при которых значения функции равны 3;7; в) найдите точку пересечения данной прямой с прямой, заданной уравнением x=4
Функция у = 2х - 1 является линейной функцией, то есть графиком данной функции будет прямая. Для построения прямой достаточно двух точек.
х = 1; у = 2 * 1 - 1 = 1. Точка (1; 1).
х = 5; у = 2 * 5 - 1 = 9. Точка (5; 9).
Чертим координатную плоскость, ставим точки, проводим прямую.
а) Значения функции - это значение у, значение аргумента - это значение х. Находим точки -2, 0 и 3 на оси х, мысленно проводим вертикальную прямую и определяем координату у в точке на прямой.
х = -2; у = -5.
х = 0; у = -1.
х = 3; у = 5.
б) Находим точки 3 и 7 на оси у, мысленно проводим горизонтальную прямую, определяем координату х на прямой.
у = 3; х = 2, точка (3; 2).
у = 7; х = 4.
в) Прямая х = 4 - это вертикальная прямая, пересекающая ось х в точке 4. Чертим данную прямую, определяем координаты точки пересечения. Точка (4; 7)