а) Выбрать 4 ромашки можно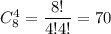 
а 3 незабудки - 
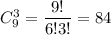По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно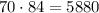 
ответ
b) Как минимум 4 незабудки это 4 незабудки или 5 незабудки или 6 незабудки или 7 незабудки.. Чувствуется что здесь правило сложения. Четыре незабудки и три ромашки можно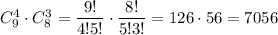 
Выбрать пять незабудки и две ромашки можно 
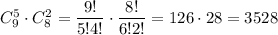Выбрать шесть цветов незабудки и одна ромашку можно 
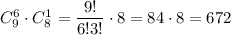И наконец выбрать семь цветов незабудки можно 
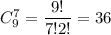По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
ответ: 11292.
4+0+...4(2-n)=2n(3-n)
Док-во: 1) Проверим, что верно n=1: 4=2*1(3-1); 4=2(2); 4=4 -верно
2)Допустим, что верно для n=k, тогда: 4+...+4(2-k)=2k(3-k)
3)Докажем, что верно для n=k+1, тогда 4+...+4(2-(k+1))=2(k+1)(3-(k+1));
4+...+4(2-1-k)=2(k+1)(3-1-k); 4+...+4(1-k)=2(k+1)(2-k) -?
4+...+4(1-k)=2(k+1)(2-k)=> {4+...+4(2-k)}+4(1-k)= то, что находится в {...} заменяем на то, что получили во втором шаге, т.е. на 2k(3-k), получаем
= 2k(3-k)+4(1-k)=6k-2k^2+4-4k= 6k-4k-2k^2+4= 2k-2k^2+4= -(2k^2-2k-4)
Раскладываем квадратное уравнение -(2k^2-2k-4)=0; D=4+32=36=6^2
k1=(2-6)/4=-4/4=-1; k2=(2+6)/4=10/4 => -(2k^2-2k-4)=-2(k-10/4)(k+1)=(-2k+5)(k+1)=
=(5-2k)(k+1)=2(2.5-k)(k+1)
Получается, что неверно, но м.б. я гдн-то ошибся, но в общем такого вида получается док-во
(-∞; (15 - √253) / 14) ∪ ((15 + √253) / 14; +∞)
Объяснение:
(3 - х)(7х + 1) < 5х + 2
21х + 3 - 7х² - х < 5x + 2
-7x² + 20x + 3 < 5x + 2
-7x² + 20x - 5x + 3 - 2 < 0
-7x² + 15x + 1 = 0
D = 15² - 4 * (-7) = 225 + 28 = 253
√D = √253
x₁ = (-15 - √253) / (-7 * 2) = -(15 + √253) / (-14) = (15 + √253)/14 (примерно 2,207)
x₂ = (-15 + √253) / (-7 * 2) = -(15 - √253) / (-14) = (15 - √253) / 14 (примерно -0,06)
начертим координатную прямую (см. рис)
подставим -1 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - (-1)) * (7 * (-1) + 1) - 5 * (-1) - 2 =
= 4 * (-7 + 1) + 5 - 2 =
= -6 * 4 + 5 - 2 =
= -24 + 5 - 2 = -21
впишем в промежутке от -∞ до (15 - √253) / 14 знак "-"
подставим 0 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - 0) * (7 * 0 + 1) - 5 * 0 - 2 = 3 * 1 - 2 = 1
впишем в промежутке от (15 - √253) / 14 до (15 + √253)/14 знак "+"
подставим 3 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - 3) * (7 * 3 + 1) - 5 * 3 - 2 = 0 - 15 - 2 = -17
впишем в промежутке от (15 + √253) / 14 до +∞ знак "-"
Неравенство принимает отрицательное значение в промежутках:
(-∞; (15 - √253) / 14) ∪ ((15 + √253) / 14; +∞)