Пусть функция 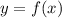 определена на отрезке
определена на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png)
Разобьём отрезок произвольным образом на n частей точками:
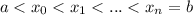
В каждом интервале произвольным образом выбираем точку
![c_{i}\in [x_{i-1};x_{i}]](/tpl/images/1361/6254/a2b9c.png)
Cумма
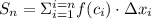 ,
,
где 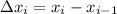 - длина частичного отрезка
- длина частичного отрезка ![[x_{i-1};x_{i}]](/tpl/images/1361/6254/3b10f.png) ,
,
называется интегральной суммой функции 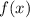 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) .
.
Определенным интегралом от функции 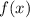 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) называется предел интегральных сумм
называется предел интегральных сумм 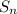 , при условии, что длина наибольшего частичного отрезка стремится к нулю
, при условии, что длина наибольшего частичного отрезка стремится к нулю
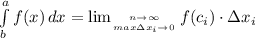
Геометрическая интерпретация определённого интеграла - площадь криволинейной трапеции
Функция y = x + 4/3 является линейной, т.к. здесь х в первой степени. Эта функция в общем виде может быть представлена как y = ax + b, где a и b - любые числа ( в нашем случае a = 1, а b = 4/3).
Функция y = x (x + 2) / x может быть преобразована в линейную только при условии, что x не равен 0 (при этом условии можно правую часть выражения сократить на х и получить y = x + 2), но в т.к. функция задана общем виде, без этого ограничения, то она не является линейной. Две последние функции содержат х в отрицательной степени (степень х равна -1), они обе не являются линейными.
я не знаю прости я давно не проходила