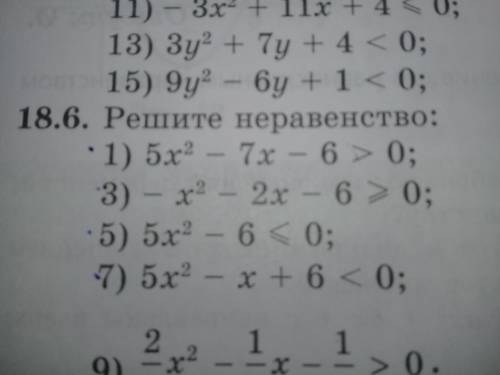
x²-(√6-√24)x-12=0
1) Упростим выражение (√6-√24).
√6-√24 = √6-√(4·6) = √6-2√6 = - √6
2) Подставим в данное уравнение и получим:
x² - (-√6)x - 12 = 0
x² + √6x - 12 = 0
3) Решаем уравнение
x² + √6x - 12 = 0
D = 6 - 4·1·(-12) = 6 + 48 = 54
√D = √54 = √(9·6) = 3√6
x₁ = (- √6 - 3√6)/2 = - 4√6/2 = - 2√6
x₂ = (- √6 + 3√6)/2 = 2√6/2 = √6
4) Находим целые числа, заключенные между корнями уравнения
x₁ = - 2√6 ≈ - 4,9
x₂ = √6 ≈ 2,45
{- 4; - 3; - 2; - 1; 0; 1; 2}
И, наконец, находим их сумму:
- 4 - 3 - 2 - 1 + 0 + 1 + 2 = - 7
ответ: - 7.
если число больше 0, и оно есть в обеих сторонах неравенства, то мы можем на него сократить без изменения знака
1. a+b>=0
a^3+b^3 >= a^b + ab^2
(a+b)(a^2-ab+b^2) >= ab(a+b) сокращаем на a+b при a+b = 0 это неравенство превращается в равенсто
a^2-ab+b^2 >= ab
a^2-2ab+b^2>=0
(a-b)^2>=0 квадрат всегда больше равен 0
2. ab>0
a/b + b/a >=2
a/b + b/a - 2 >=0
(a^2+b^2 - 2ab)/ab >=0
(a-b)^2/ab >= 0
ab>0 (a-b)^2>=0 первое по условию , второе по определению квадрата
3. ab/c + ac/b + bc/a >= a+b+c при a b c >0
(a^2b^2/abc + a^2c^2/abc + b^2c^2)/abc - abc(a+b+c)/abc >=0
знаменатель отбросим он всегда больше 0 a*b*c>0
2(a^2b^2 + a^2c^2 + b^2c^2 - a^2bc - b^2ac - c^2ab)/2 >=0
умножаем на 2 числитель и знаменатель
(a^2b^2 + a^2c^2 - 2a^2bc + a^2b^2 + b^2c^2 - 2b^2ac + a^2c^2+b^2c^2 - 2c^2ab)/2 >=0
(a^2(b^2-2bc+c^2) + b^2(a^2-2ac+c^2) + c^2(a^2-2ab+b^2))/2 >=0
(a^2(b-c)^2 + b^2(a-c)^2 + c^2(a-b)^2)/2 >=0
слева сумма квадратов деленное на положительное число, всегда больше равно 0
В решении.
Объяснение:
Решить неравенства:
1) 5х² - 7х - 6 > 0
Приравнять к нулю и решить как квадратное уравнение:
5х² - 7х - 6 = 0
D=b²-4ac =49 + 120 = 169 √D=13
х₁=(-b-√D)/2a
х₁=(7-13)/10
х₁= -6/10
х₁= -0,6;
х₂=(-b+√D)/2a
х₂=(7+13)/10
х₂=20/10
х₂=2.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -0,6 и х= 2, отметить эти точки схематично, смотрим на график.
По графику ясно видно, что у > 0 (как в неравенстве), при значениях х от - бесконечности до -0,6 и при х от 2 до + бесконечности.
Решение неравенства: х∈ (-∞; -0,6)∪(2; +∞).
Неравенство строгое, скобки круглые.
3) -х² - 2х - 6 >=0
Приравнять к нулю и решить как квадратное уравнение:
-х² - 2х - 6 =0/-1
х² + 2х + 6 =0
D=b²-4ac =4 - 24 = -20
D < 0
Уравнение не имеет действительных корней, так как парабола не пересекает ось Ох, а неравенство не имеет решения.
5) 5х² - 6 <= 0
Приравнять к нулю и решить как неполное квадратное уравнение:
5х² - 6 = 0
5х² = 6
х² = 6/5
х² = 1,2
х = ±√1,2
х₁ = √1,2 ≈ 1,1;
х₂ = -√1,2 ≈ -1,1.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -√1,2 (≈ -1,1) и х= √1,2 (≈ 1,1), отметить эти точки схематично, смотрим на график.
По графику ясно видно, что у <= 0 (как в неравенстве), при значениях х от -√1,2 до х= √1,2.
Решение неравенства: х∈ [-√1,2; √1,2].
Неравенство нестрогое, скобки квадратные.
7) 5х² - х + 6 < 0
Приравнять к нулю и решить как квадратное уравнение:
5х² - х + 6 = 0
D=b²-4ac =1 - 120 = -119
D < 0
Уравнение не имеет действительных корней, так как парабола не пересекает ось Ох, а неравенство не имеет решения.