Квадратное уравнение, решаем относительно x: Ищем дискриминант: D=(-3)^2-4*1*(-4)=9-4*(-4)=9-(-4*4)=9-(-16)=9+16=25;Дискриминант больше 0, уравнение имеет 2 корня: x_1=(√25-(-3))/(2*1)=(5-(-3))/2=(5+3)/2=8/2=4;x_2=(-√25-(-3))/(2*1)=(-5-(-3))/2=(-5+3)/2=-2/2=-1.
Корень х = 4 исключаем, так как х² - 16 ≠ 0, х ≠ +-4.
Квадратное уравнение, решаем относительно x: Ищем дискриминант: D=(-3)^2-4*1*(-4)=9-4*(-4)=9-(-4*4)=9-(-16)=9+16=25;Дискриминант больше 0, уравнение имеет 2 корня: x_1=(√25-(-3))/(2*1)=(5-(-3))/2=(5+3)/2=8/2=4;x_2=(-√25-(-3))/(2*1)=(-5-(-3))/2=(-5+3)/2=-2/2=-1.
Корень х = 4 исключаем, так как х² - 16 ≠ 0, х ≠ +-4.
|x|>5 что такое модуль: |x|=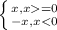
x (-
(-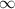 ;-5)
;-5) (5;+
(5;+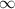 ).
).
ответ: (-\infty;-5) (5;+\infty).
(5;+\infty).
Аналогично с остальными:
|x|>=5
x (-
(-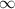 <;-5]
<;-5] [5;+
[5;+ ).
).
...
|x|<-5
По определению, модуль - неотрицательное число, значит х э пустое множество (перечеркнутый круг).
|x|<=0
По выше сказаному определяем, что х=0.
|x|>-5
Если |x|>=0, тогда
|x|>=0
x (-
(- ;+
;+ ).
).
|2х|<=6
x [-3;3].
[-3;3].
ответ: [-3;3]