1. Найти наибольшее и наименьшее значение функции
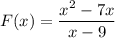на промежутке [-4; 1]
Точка разрыва x=9 в заданный интервал не входит.
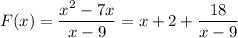
Первая производная для нахождения точек экстремумов.
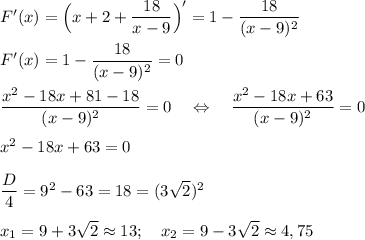
Обе точки экстремумов не попадают в интервал x∈[-4; 1]
Значения функции на концах интервала
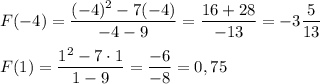
ответ: наименьшее значение функции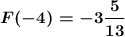 
;
наибольшее значение функции F(1) = 0,75
-----------------------------------------------------------------------------
2. Записать уравнение касательной к графику
функции F(x)=x⁴-2x в точке x₀=-1
Уравнение касательной имеет вид y = F(x₀) + F’(x₀)·(x - x₀)
F(-1) = x⁴-2x = (-1)⁴ - 2(-1) = 1+2 = 3
F'(-1) = (x⁴-2x)' = 4x³ - 2 = 4(-1)³ - 2 = -6
y = F(x₀) + F’(x₀)·(x - x₀) = 3 - 6 (x + 1) = 3 - 6x -6 = -6x - 3
ответ: уравнение касательной y = -6x - 3
---------------------------------------------------------------------------
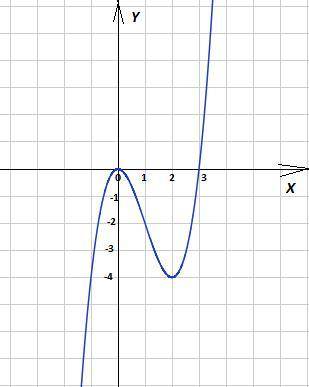
3. Исследовать функцию и построить ее график F(x)=x³-3x²
1) Область определения D(F) = R
2) Область значений E(F) = R
3) Нули функции
F(x)=x³-3x² = 0; x²(x - 3) = 0; x₁ = 0; x₂ = 3
4) Пересечение с осью OY
x = 0; F(0) = 0³-3·0² = 0
5) Экстремумы функции
F'(x) = 0; (x³-3x²)' = 0; 3x² - 6x = 0; 3x(x - 2) = 0;
x₁ = 0; F(0) = 0; F"(0) = 6x - 6 = -6 ⇒ локальный максимум.
x₂ = 2; F(2) = 2³-3·2² = -4; F"(2) = 6x - 6 = 6 ⇒ локальный минимум.
6) Монотонность функции.
Интервалы знакопостоянства первой
производной F'(x) = 3x(x - 2)
++++++++ (0) ------------- (2) +++++++++> x
/ \ /
x ∈ (-∞; 0)∪(2; +∞) - функция возрастает
x ∈ (0;2) - функция убывает
7) Функция не периодическая, общего вида (не является чётной, не является нечётной).
8) Дополнительные точки для построения
x₃ = -1; y₃ = -4; x₄ = 1; y₄ = -2
9) График функции в приложении
Общий анализ ребуса–равенства кока + кола = вода позволяет написать неравенства 1 ≤ к ≤ 4 (во-первых, к ≠ 0 как значащая цифра четырёхзначного числа; во-вторых, при к ≥ 5, результат сложения двух четырёхзначных чисел окажется пятизначным, что не возможно: «вода» – четырёхзначное число). Следовательно, в = 2 * к + 1, то есть в ϵ {3; 5; 7; 9}.
Заметим, что разряды единиц слагаемых и суммы выражены одной буквой «а». Однозначно, а = 0, так как все остальные цифры не удовлетворяют равенству а + а = а (даже с учётом перехода десятка на следующий разряд).
Такую же картину наблюдаем в разрядах сотен; однако, здесь ситуация отличается от той ситуации, которую только что рассмотрели. Теперь буква «о», по условию задания, не может быть 0 (разные буквы заменяют разные цифры). Здесь равенству о + о = о с учётом перехода ста (как результат сложения «к» десятков и «л» десятков) на следующий разряд удовлетворяет только о = 9. Следовательно: к + л ≥ 10; в ϵ {3; 5; 7} (цифру 9 исключили, поскольку она уже занята) и к ≠ 4 (иначе, буква «в» приняла бы значение 9, что не возможно).
Неравенство к + л ≥ 10 не позволяет букве «к» принимать значение 1, так как л – однозначное число и л ≠ 9.
Пусть к = 2, тогда 2 + л ≥ 10 или л ≥ 8, откуда л = 8 (так как о = 9). Следовательно, к + л = 10. Тогда, д = 0, что также невозможно, так как а = 0.
Осталось только к = 3. Теперь всё становится на своё место: в = 2 * 3 + 1 = 7; к + л = 3 + л ≥ 10 или л ≥ 7, откуда л = 8 (так как 7 и 9 уже заняты).
Таким образом, ребус «кока + кола = вода» разгадан: 3930 + 3980 = 7910.
ответ: 3930 + 3980 = 7910.
Объяснение:
