В решении.
Объяснение:
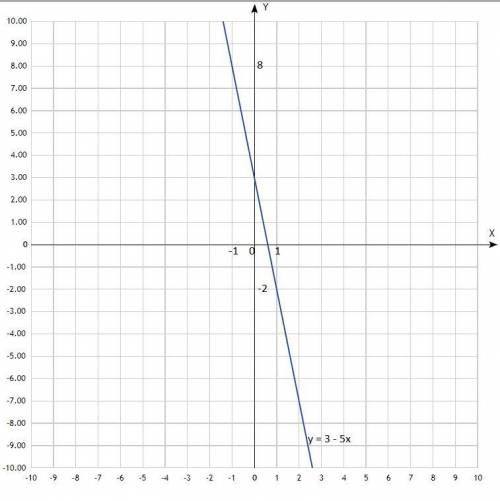
1) Постройте график функции у = 3 - 5х.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 3 - 5х
Таблица:
х -1 0 1
у 8 3 -2
По вычисленным точкам построить прямую.
2) Проходит ли график функции у = -5х + 4 через точку М(-7; 39)?
Нужно подставить известные значения х и у (координаты точки) в уравнение. Если левая часть равна правой, то проходит, и наоборот.
у = -5х + 4; М(-7; 39);
39 = -5*(-7) + 4
39 = 39, проходит.
3) Дана функция у = 1/4 х - 8. Найти значение функции, если значение аргумента равно 12.
Проще, найти значение у, если х = 12.
Подставить значение х в уравнение и вычислить у:
у = х/4 - 8
у = 12/4 - 8
у = 3 - 8
у = -5;
При х = 12 у = -5.
x=12, min((16/x)+(x/9))=8/3
Объяснение:
Часть теоремы о средних - неравенство между средним арифметическим и средним геометрическим(неравенство Коши)
(16/x)+(x/9)≥2√((16/x)(x/9))=2√(16/9)=2·4/3=8/3
Равенство достигается при 16/x=x/9⇔x²=144⇔x=±12
x>0⇒x=12
min((16/x)+(x/9))=8/3
Можно решить и другим
Рассмотрим функцию f(x)=16/x+x/9 при x>0. Найдём промежутки её монотонности.
f '(x)=-16/x²+1/9=(x²-144)/(9x²)=(x-12)(x+12)/(9x²)
x∈(0;12)⇒f '(x)<0⇒f↓
x∈(12;+∞)⇒f '(x)>0⇒f↑
minf(x)=f(12)=16/12+12/9=4/3+4/3=8/3
x∈(0;+∞)