ответ: (cos2x - sin^2x) / (2 * sin^2x - cos^2x) = - 1.
Объяснение:
1. Для того что бы упростить данное тригонометрическое выражение нам понадобится знание основных тригонометрических формул. В этом тригонометрическом выражении мы будем использовать вот эту формулу:
cos^2a + sin^2a = 1;
2. Подставим формулу cos^2a + sin^2a = 1, в тригонометрического выражения, получаем:
(cos2x - sin^2x) / (2 * sin^2x - cos^2x) = (cos^2a - sin^2a - sin^2a) / (2 * sin^2x - cos^2x) =
= ( - 2 * sin^2a + cos^2a) / (2 * sin^2x - cos^2x) =
= - (2 * sin^2x - cos^2x) / (2 * sin^2x - cos^2x) = - 1.
7; -4
Объяснение:
Решение методом подбора корней:
Записываем исходное уравнение:
(х - 7)(х + 4) = 0
Подбираем х:
х1 = 7, х2 = -4
Решение через раскрытие скобок, теорему Виета, и дискриминант:
Записываем исходное уравнение:
(х - 7)(х + 4) = 0
Раскрываем скобки:
х*х - 7x + 4x - 28 = 0
x^2 - 7x + 4x - 28 = 0
Приводим подобные:
x^2 - 3x - 28 = 0
1 под
Решаем через теорему Виета:
x1 + x2 = 3
x1*x2 = -28
Откуда:
x1 = 7, x2 = -4
2 под Решение через дискриминант
Записываем исходное уравнение:
x^2 - 3x - 28 = 0
Ищем дискриминант:
D = b^2 - 4ac
D = (-3)^2 -4*1*(-28)
D = 9 - (-112)
D = 9 + 112 = 121
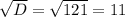
Находим корни уравнения:
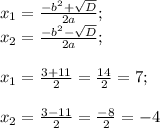
В данном решении показано решения данного уравнения. (причем имеет 2 под
Сначала надо преобразовать выражение 2х+у=3, выделив у
у = -2х + 3
у - функция, х - аргумент.
Видно, что функция линейная, т.к. содержит х в 1-й степени.
Графиком линейной функции является прямая.
Прямая строится по 2-м точкам.
При х = 0 у = 3 - вот вам 1-я точка.
При у = 0 у = -2х + 3 найдём х
0 = - 2х + 3
2х = 3
х = 1,5
Вот и 2-я точка: х = 1,5, у = 0
Теперь чертим прямоугольную систему координат у - вертикальная ось, х - горизонтальная.
На оси у откладываем 3, это и будет 1-я точка, на оси х откладываем1,5 это 2-я точка.
Через две отмеченные точки проводим прямую
Вот и всё.