Объяснение:
Сначала решим уравнение четвертой степени.
По теореме Безу его корни надо искать среди делителей свободного члена (в нашем случае свободный член равен 24)
Простым подбором, получаем 2 корня:
x = -2 и x= -3
Далее найдем произведение:
(x+2)·(x+3) = x² + 5x + 6
Разделим исходное уравнение на полученное произведение "столбиком"
Итак, неравенство можно написать так:
(x+2)(x+3)(x²+4) > 0
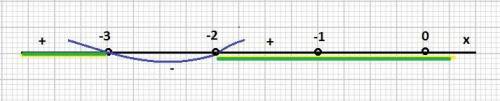
Поскольку (x²+4)>0, то по правилу интервалов находим решение неравенства:
(x+2)(x+3)>0
Получили:
x ∈ (-∞; - 3) ∪ (-2; +∞)

Пусть х км/ ч скорость второго авто, тогда х+10 (км/ч) скорость первого авто. Расстояние каждый из них в 560 км, по времени составляем уравнение:
560 / х - 560/ (х+10) = 1
Приводим к общему знаменателю х(х+10) и отбрасываем его заметив, что х не=0 и х не=-10
Получаем:
560(х+10)-560х=х(х+10)
560х+5600-560х=х^2+10х
х^2+10х-5600=0
Д= 100+4*5600=22500 , 2 корня
х(1) = (-10+150)/2= 70 х(2)=(-10-150)/2 =-80 не м.б скоростью( не подходит под условие задачи)
70+10=80 км/ч скорость первого авто
ответ: 70 и 80 км/ч скорости автомобилей.
1. 7x²+5x=0
x(7x+5)=0
x¹=0
7x+5=0
7x=-5
x²=-5/7
2. x²-6x-16=0
D=b²-4ac=36+64=100
x=-b±√D/2a=6±√D/2
x¹=6+10/2=8
x²=6-10/2=-2
3. 15x²-4x-3=0
D=b²-4ac=16+180=196
x=-b±√D/2a=4±√196/30
x¹=4+14/30=0,6
x²=4-14/30=-1/3
4. x²-7x+4=0
D=b²-4ac=49-16=33
x=-b±√D/2a=7±√33/2
x¹=7+√33/2
x²=7-√33/2
5. x²+5x+9=0
D=b²-4ac=25-36=-9
нет корней