Пусть C — первая деталь окажется стандартной. Гипотезы:
H₁ - деталь изготовлена первым заводом;
H₂ - деталь изготовлена вторым заводом;
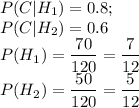
Вероятность события А по формуле полной вероятности
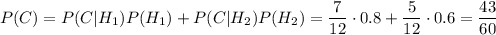
По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:
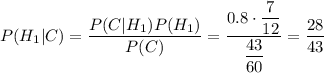
Аналогично, пусть В — вторая деталь окажется стандартной. Так как одна деталь уже вынута, то в партии остается 119 лампочек, из них 69 изготовлены на первом заводе.
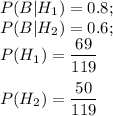
По формуле полной вероятности, вероятность события В:
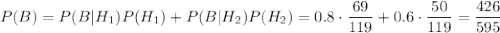
По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:
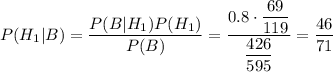
По теореме умножения, вероятность того, что наудачу взятые две лампочки являются стандартными, равна
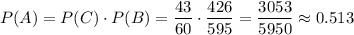
По теореме умножения, вероятность того, что обе лампочки изготовлены на первом заводе, при условии что событие А произошло, равна:
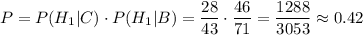
Объяснение:
Формула бинома Ньютона:
(а+b)^n=C(n,0)•a^n •b^0 +C(n,1)•a^(n-1) •b^1 +C(n,2)•a^(n-2) •b^2+...+C(n,n)•a^0 •b^n
(√5 +√2)^4=1•√5^4 •√2^0 +4•√5^3 •√2^1 +6•√5^2 •√2^2 +4•√5^1 •√2^3 +1•√5^0 •√2^4=25+20√10 +60+8√10 +4=89+28√10
(√6 +√2)^4=1•√6^4 •√2^0 +4•√6^3 •√2^1 +6•√6^2 •√2^2 +4•√6^1 •√2^3 +1•√6^0 •√2^4=36+24√12 +72+8√12 +4=112+32√12=112+64√3
(√6 -√2)^5=1•√6^5 •√2^0 -5•√6^4 •√2^1 +10•√6^3 •√2^2 -10•√6^2 •√2^3 +5•√6^1 •√2^4 -1•√6^0 •√2^5=36√6 -180√2 +120√6 -120√2 +20√6 -4√2=176√6 -304√2
(√10 -√2)^5=1•√10^5 •√2^0 -5•√10^4 •√2^1 +10•√10^3 •√2^2 -10•√10^2 •√2^3 +5•√10^1 •√2^4 -1•√10^0 •√2^5=100√10 -500√2 +200√10 -200√2 +20√10 -4√2=320√10 -704√2
9-3+14x^2-15+2+25=0 (складываем числа)
получается 18+14x^2=0