1. -15 ≤ 1-2у ≤ 0
2. 
Объяснение:
1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
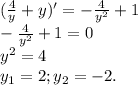
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2: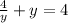 
.
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
для у=1/2 :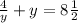 
для у=8: .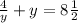
Т.е. имеем кривую с максимумами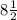 
и минимумом 4.
Тогда
Решение.
С помощью формулы Герона посчитаем площадь данного треугольника. Полупериметр равен
\rho= дробь, числитель — 11 плюс 12 плюс 7, знаменатель — 2 =15.
Тогда площадь равна
S= корень из { \rho(\rho минус 11)(\rho минус 12)(\rho минус 7)}= корень из { 15 умножить на 4 умножить на 3 умножить на 8}=12 корень из { 10}.
Далее найдем высоту через площадь и сторону треугольника. Наименьшая высота проведена к наибольшей стороне, поэтому
h= дробь, числитель — 2 умножить на S, знаменатель — 12 = дробь, числитель — 2 корень из { 10}, знаменатель — 7 .
Подставляя значение 3,16 вместо корень из { 10}, получаем:
h\approx 2 умножить на 3,16=6,32.
ответ: 6,32.