
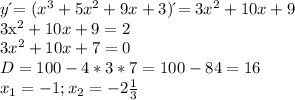

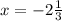
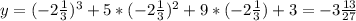
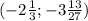 :
: (НЕТ)
(НЕТ)x^3=4y
y=x
y=(x^3)/4 и у=х
найдем точки пересечения
система:
y=x
y=(x^3)/4
x=(x^3)/4
4x=x^3
4=x^2
x1=2
x2=-2
и общая точка-начало координат, через которую проходит прямая и гипербола (0;0)
Площадь:
0 2 0 2
S(-x+(x^3)/4)dx+ S(x-(x^3)/4)dx=(-(x^2)/2+(x^4)/16))/+((x^2)/2-(x^4)/16))/= (-0+0-(-4/2+16/16))+(4/2-16/16-0-0)=2-1+2-1=2
-2 0 -2 0
-4 и -6
Объяснение:
Находим дискриминант:
D=b2-4ac
D=100-4*1*24=100-96=4
корень из 4=2
Находим корни:
x1=-10+2/2=-8/2=-4
x2=-10-2/2=-12/2=-6