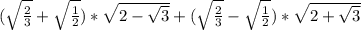
Объяснение:
Принимаем всю работу за единицу (1). ⇒
Скорость выполнения работы одним мастером равна 1/12.
Скорость выполнения работы тремя мастерами равна 3/12=1/4.
Скорость выполнения работы одним учеником равна 1/30.
Скорость выполнения работы учеников впятером равна 5/30=1/6. ⇒
Скорость выполнения работы, когда работают 3 мастера и 5 учеников
одновременно равна:
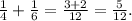
Таким образом, 3 мастера и 5 учеников работая вместе, выполнят работу за: 1:(5/12)=12/5=2,4 (дня).
ответ: 3 мастера и 5 учеников работая вместе,
выполнят работу за 2,4 дня.
1) х= -1
2)х=0
1) возведём в куб обе чести уравнения
![(\sqrt[3]{x^3+x+1})^3 =x^3](/tpl/images/1702/0238/6ff01.png)
х³+х+1=х³; ( перенесём все иксы(х) влево, а цифры -вправо)
х³+х-х³= -1;
х= - 1.
2.
Сначала найдём ОДЗ ( область действительных значений х, потому что выражение под корнем может быть больше или равно нулю).
ОДЗ : 3х+4≥0; и 2-х≥0
3х≥-4; -х≥-2
х≥ -4/3 х≤2
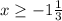 . х≤2
. х≤2
D= x ∈ [-1 1/3;2}
Теперь решаем уравнение : возведём в квадрат обе части уравнения
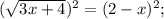
3х+4=4-4х+х₂;
3x+4-4+4x-x²=0;
-х²+7х=0;
х( 7-х)=0;
( произведение равно нулю, если хоть один член равен 0)
х=0 или 7-х=0
х₁=0 или х₂=7 - этот корень недействителен так как должен біть х≤2
ответ х=0
Есть второй вариант решения: графический
При решении были применены формулы сложного радикала :