Две бригады, работая вместе выполняют некоторую работу за 2 дня. За сколько дней эту работу выполнила бы каждая бригада в отдельности, если первой бригаде на это нужно на 3 дня больше, чем второй?
Решение.
Пусть за 
дней всю работу выполнила бы первая бригада, тогда
за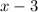 
дней всю эту работу выполнила бы вторая бригада.
Примем весь объём работы за 1 (единицу), тогда
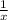- производительность первой бригады;
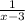- производительность первой бригады.
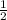- общая производительность двух бригад.
Уравнение:
(
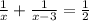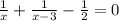
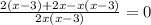
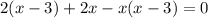
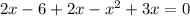
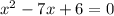
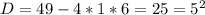
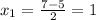
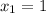не удовлетворяет условию, т.к.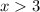 
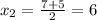
удовлетворяет условию.
За 6 дней всю работу выполнила бы первая бригада.
За 6-3=3 дня всю эту работу выполнила бы вторая бригада.
ответ: 6 дней; 3 дня.
Тангенс угла наклона касательной равен производной в точке касания к графику функции.
tgα = y'(x).
1) y = 0,2x^2 + 2x - 4, A(2; 0,8).
Проверяем - принадлежит ли точка данной функции.
0,2*2² + 2*2 - 4 = 0,8. Да, принадлежит.
Находим производную: y' = 0,2*2x + 2.
y'(2) = 0,2*2*2 + 2 = 2,8.
ответ: tgα = 2,8.
2) y = -3x^2 - x + 5, А(-2; -5).
Аналогично проверяем - точка А на кривой (парабола).
y' = -6x - 1,
y'(-2) = -6*(-2) - 1 = 12 - 1 = 11.
ответ: tgα = 11.
3) y = (x^2 - 1)/(x - 5), A(3; 3 2/3). (Ели так дано задание)
В этой задаче сложное решение, так как точка А не лежит на кривой.
Производная : y' = (2x(x - 5) - 1*(x^2 - 1))/(x - 5)^2) = (x^2 - 10x + 1)/((x - 5)^2).
Производная в точке касания хо: (xо^2 - 10xо + 1)/((xо- 5)^2).
Получим уравнение касательной проходящей через точку A(3;3 2/3):
3 2/3 = ((xо^2 - 10xо + 1)/((xо- 5)^2))(3 - хо) + ((xо^2 - 1)/(xо - 5)).
Решение затруднено, так функция - кубическая.
Ориентировочно решение найдено графически в программе ГеоГебра: у = -18,76х + 59,95.
График приведен во вложении.
.......................
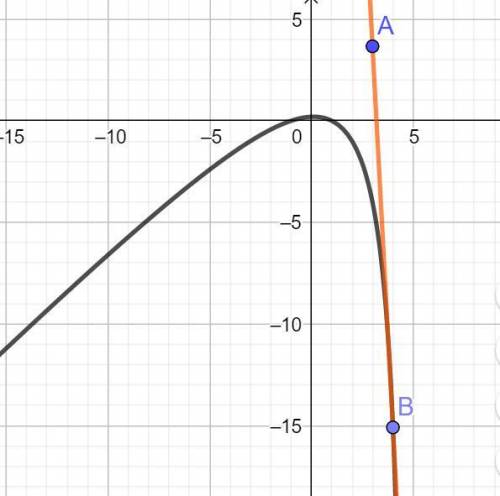