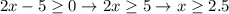
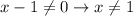
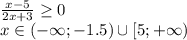
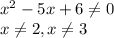
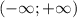Дайте определения термина- значение выражения. только коротко и чтобы было понятно заранне ! а и еще определение термина числовое выражение! тож коротко!

👇

Ответ:

varvara083017

04.06.2023

алгебраическое выражение-это одна или несколько алгебраических величин (чисел и букв), соединенных между собой знаками алгебраических действий

числовые выражения-это выражения состоящие только из цифр и знаков действия

4,6(65 оценок)

Открыть все ответы

Ответ:

lele4

04.06.2023

1. а) Выражение под корнем всегда неотрицательно. Тогда D(y): $2x-5 \geq 0 \rightarrow 2x \geq 5\rightarrow x \geq 2.5$
б) Выражение в знаменателе не равно нулю. Тогда D(y): $x-1 \neq 0\rightarrow x \neq 1$
в) Выражение под корнем всегда неотрицательно. Тогда D(y): $\frac{x-5}{2x+3} \geq 0 \\ x\in (-\infty; -1.5)\cup [5; +\infty)$
г) Выражение в знаменателе не равно нулю. Тогда D(y): (решение квадратного уравнение расписывать не буду, это алгоритм) $x^2 - 5x + 6 \neq 0 \\ x \neq 2, x \neq 3$

2. а) D(y) = $(-\infty; +\infty)$ (знаменатель в ноль не обращается) - симметричное множество.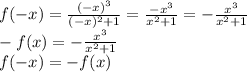
$f(-x)= \frac{(-x)^3}{(-x)^2+1} = \frac{-x^3}{x^2+1} = - \frac{x^3}{x^2+1} \\ -f(x)= - \frac{x^3}{x^2+1} \\ f(-x)=-f(x)$
Функция нечётная
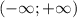б) D(y) = $(-\infty; +\infty)$ (ограничений нет) - симметричное множество.
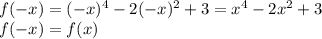
$f(-x)=(-x)^4-2(-x)^2+3 = x^4-2x^2+3 \\ f(-x)=f(x)$
Функция чётная
в) D(y) = $(-\infty; +\infty)$ (ограничений нет) - симметричное множество.
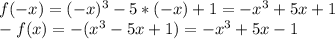
$f(-x)=(-x)^3-5*(-x)+1=-x^3+5x+1 \\ -f(x)= -(x^3 - 5x + 1) = -x^3 + 5x - 1$
Функция общего вида

3. а) Это прямая, k > 0, значит, функция всегда возрастает
б) Это прямая, k < 0, значит, функция всегда убывает
в) Это парабола, a > 0 (ветви направлены вверх), вершина имеет координату 0 по x (-b/2a = -0/4 = 0), значит, на (-∞; 0] убывает, на [0; +∞) возрастает
С3 . cамое большое кол-во . срочо. 1. найти область определения функции а) y =√(2x - 5) б) y = 6/(x

С3 . cамое большое кол-во . срочо. 1. найти область определения функции а) y =√(2x - 5) б) y = 6/(x

4,6(47 оценок)

Ответ:

prvvk

04.06.2023

Чтобы уравнение имело действительное решение , достаточно чтобы дискриминант был неотрицательным.

D/4 = (a^3-b^3)^2 -(a^2-b^2)*(a^4-b^4)>=0

То есть , необходимо доказать , что при любых a и b справедливо строгое неравенство :

(a^3-b^3)^2>=(a^2-b^2)*(a^4-b^4)

(a-b)^2*(a^2+ab+b^2)^2>=(a-b)^2* (a+b)^2 * (a^2+b^2)

Заметим , что когда a=b , получаем что 0=0 , то есть условие выполнено. И в этом случае уравнение имеет бесконечно много решений.

Теперь, поскольку мы разобрали этот случай и (a-b)^2>=0 , то для случая a≠b , можно поделить обе части неравентсва на (a-b)^2 не меняя знак неравенства :

(a^2+ab+b^2)^2>=(a+b)^2*(a^2+b^2)

( a^2+ab+b^2)^2 >= (a^2+2ab+b^2)*(a^2+b^2)

Теперь сделаем слудующий прием , поскольку (a^2+b^2)^2>0 при a≠b≠0

То можно поделить на это выражение обе части неравенства не меняя его знак :

( 1+ ab/(a^2+b^2) )^2>= 1+ 2ab/(a^2+b^2)

Тогда можно сделать замену:

ab/(a^2+b^2)=t

(1+t)^2>=1+2t

t^2+2t+1>=1+2t

t^2>=0 (верно)

Таким образом :

(a^3-b^3)^2>=(a^2-b^2)*(a^4-b^4) , то есть D>=0.