Найдите точки экстремума функции y = f(x) (48.3—48.5): 2) f(x) = -x + 9;

48.4.
2) f(x) = х2 - 3x + 10;

2) f(x) = - x3 – 8;

Question

Алгебра: Найдите точки экстремума функции y = f(x) (48.3—48.5): 2) f(x) = -x + 9; 48.4. 2) f(x) = х2 - 3x + 10; 2) f(x) = - x3 – 8; ​

ThePashka · Accepted Answer

т.к. рациональное число - это число которое можно представить в виде дроби m/n, где m - целое, а n -натуральное

т.о. частное двух рациональных чисел

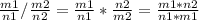
$\frac{m1}{n1} / \frac{m2}{n2} = \frac{m1}{n1} * \frac{n2}{m2} = \frac{m1*n2}{n1*m1}$

однако результатом умножения целого числа на натуральное является целое число, а не натальное, таким образом наше частное представляется в виде дроби из двух ЦЕЛЫХ чисел - это не удовлетворяет определению рационального числа.

Вывод: частное двух рациональных чисел НЕ есть число рациональное

пример первое число 1/2 - рациональное, второе число 0/5 - рациональное, частное 5/0 - не в коей мере рациональным не является

Найдите точки экстремума функции y = f(x) (48.3—48.5): 2) f(x) = -x + 9;48.4. 2) f(x) = х2 - 3x + 10;2) f(x) = - x3 – 8;​

MOGZ ответил

Найдите точки экстремума функции y = f(x) (48.3—48.5): 2) f(x) = -x + 9;

48.4.
2) f(x) = х2 - 3x + 10;

2) f(x) = - x3 – 8;