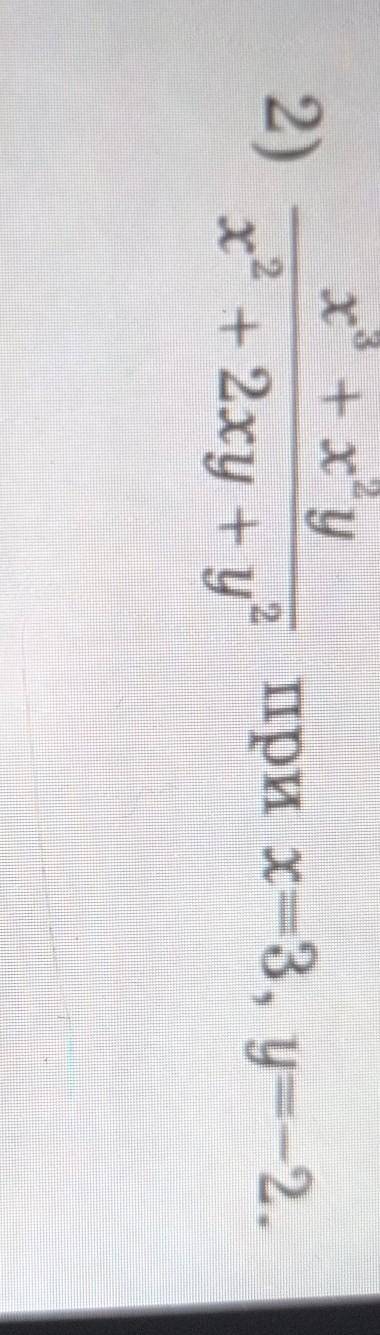
очень сильно , кто буду благодарна

Question

Алгебра: очень сильно , кто буду благодарна​

Dinka1597 · Accepted Answer

1) Пусть

- длина, тогда x-2

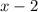- ширина. Проведём диагональ в прямоугольнике, получаем прямоугольный треугольник. Исходя из этого мы получаем уравнение по теореме Пифагора.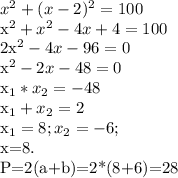
$x^{2} + (x-2)^{2}=100

 x^{2}+ x^{2} -4x+4=100

 2x^{2}-4x-96=0

 x^{2} - 2x-48=0

 x_{1}* x_{2} =-48

x_{1} + x_{2} =2

 x_{1} =8; x_{2} =-6; 

 x=8.

P=2(a+b)=2*(8+6)=28

$
ответ: периметр равен 28.

2) Нам дан прямоугольный треугольник ABC, где AB - гипотенуза, AC и BC - катеты. Пусть

- катет CB, тогда гипотенуза AB - 32-x

. Составим уравнение по теореме Пифагора.
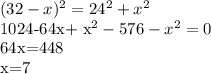
$(32-x)^2=24^2+x^2

1024-64x+ x^{2}-576- x^{2}=0

64x=448

x=7$
Мы нашли катет CB, а значит гипотенуза AB=25.
ответ: AB=25, CB=7.

3) Пусть

- большее число, тогда x-6

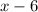- меньшее число. Составим уравнение, зная произведение этих чисел.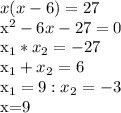
$x(x-6)=27

 x^{2}-6x-27=0

 x_{1} * x_{2}=-27

 x_{1} + x_{2}=6

 x_{1}=9: x_{2}=-3

 x=9$
Мы нашли первое число, теперь найдём второе.
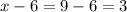x-6=9-6=3

.
ответ: 3 и 9.

очень сильно , кто буду благодарна​

MOGZ ответил