Больше не добавляйте вопрос в котором больше 3 пример так как дальше можно отметить "Много решений".
x³+4x²-x-4=0
x²*(x+4)-(x+4)=0
x+4)*(x²-1)=0
x+4=0
x²-1=0
x=-4
x=-1
x=1
x₁=-4, x₂=-1, x₃=1
______________
x³-2x²-15x=0
x*(x²-2x-15)=0
x*(x²+3x-5x-15)=0
x*(x*x+3)-5(x+3))=0
x*(x+3)*(x-5)=0
x=0
x+3=0
x-5=0
x=0
x=-3
x=5
x₁=-3, x₂=0, x₃=5
_____________
(2x-5)²*(x-5)=(2x-5)*(x-5)²
(2x-5)²*(x-5)-(2x-5)*(x-5)²=0
(2x-5)*(x-5)*(2x-5-x(x-5))=0
(2x-5)*(x-5)*(2x-5-x+5)=0
(2x-5)*(x-5)x=0
2x-5=0
x-5=0
x=0
x=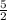
x=5
x=0
x₁=0, x₂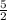 ,x₃=5
,x₃=5
Альтернативная форма:
x₁=0, x₂=2,5, x₃=5
______________
(x-1)*(x²+8x+16)=6(x+4)
x³+8x²+16x-x²-8x-16=6x+24
x³+7x²+8x-16=6x+24
x³+7x²+8x-16-6x-24=0
x³-2x²+9x²+2x-40=0
x³-2x²+9x²-18x+20x-40=0
x²*(x-2)+9x*(x-2)+20(x-2)=0
(x-2)*(x²+9x+20)=0
(x-2)*(x²+5x+4x+20)=0
(x-2)*(x*(x+5)+4(x+5))=0
(x-2)*(x+5)*(x+4)=0
x-2=0
x+5=0
x+4=0
x=2
x=-5
x=-4
x₁=-5, x₂=-4, x₃=2
______________
x⁴=(4x-5)²
x²=|4x-5|
x²-|4x-5|=0
x²-(4x-5)=0 , 4x-5≥0
x²-(-(4x-5))=0 , 4x-5<0
x∉R,x≥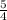
x=-5
,x<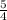
x=1
x∉R
x=-5
x=1
x₁=-5, x₂=1
Если мой ответ вас устраивает выбрать его наилучшим
Объяснение:
Рассмотрим функцию y = (23 - x) * e23 – x. Отметим, что данная функция определена и дифференцируема для всех х ∈ (-∞; +∞). По требованию задания, найдём точки минимума данной функции, если таковые существуют. Воспользуемся приёмами дифференциального и интегрального исчисления. Как известно, необходимым условием экстремума функции одной переменной в точке x* является равенство нулю первой производной функции, то есть, в точке x* первая производная функции должна обращаться в нуль.
Найдём первую производную данной функции: f Ꞌ(x) = ((23 - x) * e23 – x)Ꞌ = (23 - x)Ꞌ * e23 – x + (23 - x) * (e23 – x)Ꞌ = -e23 – x - (23 - x) * e23 – x = (x – 24) * e23 – x. Приравнивая производную к нулю, получим уравнение (x – 24) * e23 – x = 0. Для того, чтобы произведение двух сомножителей равнялось нулю, необходимым и достаточным условием является равенство нулю хотя бы одного из сомножителей. Поскольку для любого х ∈ (-∞; +∞) справедливо e23 – x > 0, то получим х – 24 = 0, откуда х = 24.
Для выяснения поведения функции в найденной точке, рассмотрим поведение производной в следующих двух множествах: (-∞; 24) и (24; +∞). Очевидно, что, при х ∈ (-∞; 24), например, при х = 23, производная f Ꞌ(x) < 0; при х ∈(24; +∞), например, при х = 25, производная f Ꞌ(x) > 0.
Поскольку при переходе через точку х = 24 производная f Ꞌ(x) меняет свой знак с минуса на плюс, то точка x = 24 является точкой минимума функции. Вычислим значение данной функции при x = 24. Имеем: f(24) = (23 - 24) * e23 – 24 = -1 / е.
Значит, точкой минимума данной функции является х = 24.
ответ: Точкой минимума данной функции является х = 24.