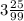
Объяснение:
3,(25)
Чтобы обратить периодическую дробь в обыкновенную достаточно записать в числителе период , а в знаменателе записать стольно девяток, сколько цифр в периоде
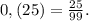
Значит
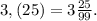
Обозначим данное число через x
x=3,(25) = 3,252525... .(1)
Умножим обе части данного равенства на 100
100x = 325,252525... .(2)
Вычтем почлено из уравнения (2 ) уравнение (1), получим
99x= 322;
x=322:99;
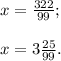
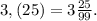
Представим данное число в виде суммы
3,252525...= 3+0,25+0,0025+0,000025+...
Сумма 0,25+0,0025+0,000025+... представляем сумму бесконечной геометрической прогрессии
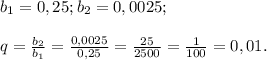
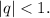
Найдем сумму бесконечно убывающей геометрической прогрессии по формуле
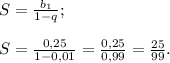
Тогда
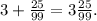
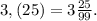
Объяснение:Скорость парохода в стоячей воде обозначим v км/ч. Скорость течения нам известна - 4 км/ч. По течению пароход км со скоростью v + 4 км/ч, против течения еще 48 км со скоростью v - 4 км/ч, и затратил на все это 5 ч времени. Составляем уравнение: 48/(v + 4) + 48/(v - 4) = 5 переносим 5 влево и приводим к общему знаменателю: [ 48*(v - 4) + 48*(v + 4) - 5(v + 4)(v - 4) ] / [ (v + 4)(v - 4) ] = 0 Числитель приравниваем к 0 и раскрываем скобки: 48v - 4*48 + 48v + 4*48 - 5(v^2 - 16) = 0 Раскрываем скобки и приводим подобные: 96v - 5v^2 + 80 = 0 Меняем знак: 5v^2 - 96v - 80 = 0 D/4 = 48^2 + 5*80 = 2304 + 400 = 2704 = 52^2 v1 = (48 - 52) / 5 < 0 v2 = (48 + 52) / 5 = 20 ответ: 20 км/ч.
б)3a-7b-6a+8b=-3a+b
в)10x-(3x-1)+(x-4)=10x-3x+1+x-4=8x-3