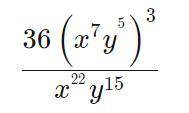
Упростим выражение.
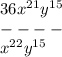
Сократим x²¹ полностью.
От x²² останется просто х.
y сокращается полностью.
Остаётся: 36/х
36/-12= - 3
ответ: -3.
В решении.
Объяснение:
Сравнить:
1) 4,7*10^-6 и 5,9*10^-7;
4,7*10⁻⁶ и 5,9*10⁻⁷;
1/4,7⁶ и 1/5,9⁷;
1/4,7⁶ > 1/5,9⁷;
Чем больше знаменатель, тем меньше значение дроби.
2) 1,23*10^6 и 0,12*10^7;
1,23*10⁶ и 0,12*10⁷;
Привести второе число к стандартному виду:
1,23*10⁶ и 1,2*10⁶;
1,23*10⁶ > 1,2*10⁶;
Если показатели степени одинаковые, больше то число, основание которого больше.
3) 31,6*10^-8 и 0,061*10^-8;
31,6*10⁻⁸ и 0,061*10⁻⁸;
1/31,6⁸ и 1/0,061⁸;
Привести оба знаменателя к стандартному виду:
1/3,16⁹ и 1/6,1⁶;
1/3,16⁹ < 1/6,1⁶;
Чем больше знаменатель, тем меньше значение дроби.
Объяснение:
Система уравнений:
x/2 +y/2 -2xy=16 |×2
x+y=-2
x+y-4xy=32
-2-4xy=32
-4xy=32+2
-4xy=34 |2
x=-17/(2y)
-17/(2y) +y=-2
(-17+2y²)/(2y)=-2
-17+2y²=-4y
2y²+4y-17=0; D=16+136=152
y₁=(-4-2√38)4=(-2-√38)/2
y₂=(-4+2√38)4=(√38 -2)/2
x₁+(-2-√38)/2=-2; x₁=(-4+2+√38)/2=(√38 -2)/2
x₂+(√38 -2)/2=-2; x₂=(-4-√38 +2)/2=(-2-√38)/2
ответ: ((√38 -2)/2; (-2-√38)/2); ((-2-√38)/2; (√38 -2)/2).
Система уравнений:
x/2 +y/2 +2xy=4
x-y=4
x/2 +y/2 +2xy=x-y |×2
x+y+4xy=2x-2y
4xy=2x-2y-x-y
4xy=x-3y
x-4xy=3y
x(1-4y)=3y
x=(3y)/(1-4y)
(3y)/(1-4y) -y=4
(3y-y+4y²)/(1-4y)=4
2(y+2y²)=4(1-4y) |2
2y²+y-2+8y=0
2y²+9y-2=0; D=81+16=97
y₁=(-9-√97)/4
y₂=(-9+√97)/4=(√97 -9)/4
x₁ -(-9-√97)/4=4; x₁=(16-9-√97)/4=(7-√97)/4
x₂ -(√97 -9)/4=4; x₂=(16+√97 -9)/4=(7+√97)/4
ответ: ((7-√97)/4; (-9-√97)/4); ((7+√97)/4; (√97 -9)/4).
Подставим x = –12, y = 0,8:
ответ: –3.