если b[1], b[2], b[3], .. - данная бесконечная убывающая геомметрическая прогрессия с знаменателем q, то
последовательность составленная из квадратов членов данной, тоже бессконечная убывающая c первым членом b[1] и знаменателем q^2
используя формулу суммы бесконечной убывающей прогрессии
b[1]/(1-q)=4
b[1]^2/(1-q^2)=48
откуда разделив соотвественно левые и правые части равенств, и используя формулу разности квадратов
b[1]^2/(1-q^2) :b[1]/(1-q)=48/4
b[1]/(1+q)=12
откуда
b[1]=12(1+q)=4(1-q)
12+12q=4-4q
12q+4q=4-12
16q=-8
q=-1/2
b[1]=4*(1-(-1/2))=4+2=6
1). x²+3x+2=(x-...)(x+1)
Найдём иксы уравнения:
D = 3²-4·2 = 9-8 = 1
Подставляем по формуле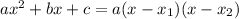 :
:
x²+3x+2=(x+2)(x+1)
2). 2x²-3x+1=2(x-1)(x-...)
Найдём иксы уравнения:
D = -3²-4·2 = 9-8 = 1
Подставляем по формуле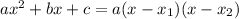 :
:
2x²-3x+1=2(x-1)(x-0,5).