
Чтобы вычислить площадь фигуры, ограниченной графиком функции 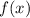 на заданном промежутке
на заданном промежутке ![[a; \ b]](/tpl/images/1350/2276/cd2bf.png) , следует найти определенный интеграл:
, следует найти определенный интеграл:
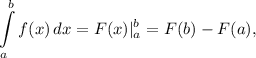
где 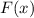 — первообразная для функции
— первообразная для функции 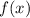
1) Имеем функцию 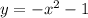 и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке
и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке ![[1; \ 2]](/tpl/images/1350/2276/2bc6a.png)
Найдем определенный интеграл, приписав перед ним знак "минус", поскольку график функции находится под осью абсцисс:
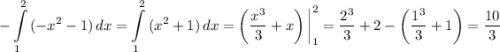
2) Вычислим площадь фигуры, ограниченной графиками функций 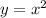 и
и 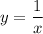 на отрезке
на отрезке ![[1; \ 3]](/tpl/images/1350/2276/24e94.png)
Чтобы найти эту площадь, следует вычислить определенный интеграл разности функций 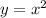 и
и 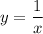 (только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):
(только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):
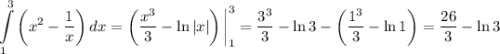
ответ: 1) 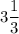 кв. ед.; 2)
кв. ед.; 2) 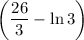 кв. ед.
кв. ед.