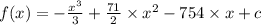
Объяснение:
Предположим что производственной функции является квадратное уравнение.
Знаем что экстремум функции это когда производная этой функции равна нулю.
1) Зная корни производной (13 и 58) запишем его и проверим возрастание и убывание функции:
f'(x) = (x-13)*(x-58)
f'(0)=(0-13)*(0-58)=754
f'(14)=(14-13)*(14-58)=-44
Данные условия не соблюдаются. Так как 13 является максимум, а 58 минимум функции.
Умножим производную на - 1.
2)
f'(x) = -1*(x-13)*(x-58)
f'(0)= - 1*(0-13)*(0-58)=-754
f'(14)= - 1*(14-13)*(14-58)=44
Условия соблюдаются.
3) Найдем первообразную функции
f'(x) = -1*(x-13)*(x-58)=-x^2+71*x-754
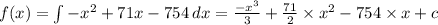
х=100%, тоді 30% від початкового числа будуть дорівнювати 0,3х.
Початкове число збільшили на 30 відсотків, тому число яке отримали буде дорівнювати х+0,3х=1,3х.
Потім зменшили число на 30%, але зауважу, зменшили не початкове число, а те число, яке ми отримали, тому це буде 30% від 1,3х.
100%=1,3х
30%=
Оскільки наше число зменшили, то отримане число буде дорівнювати 1,3х-0,39х=0,91х .
Початкове число 1х, а отримане 0,91х. 1х-0,91х=0,09х отже число зменшилося на 9%.
Відповідь: зменшиться на 9%