Решено верно :) надеюсь поймешь!
Объяснение:
Система решена точно правильно.
Получаем ответ: (4:5)
х=4 (1 слиток олова)
у=5 (1 слиток свинца)
Удачи, надеюсь
прощения за кривой почерк)
Система решена методом сложения.
Пояснение:
Ты должна в ОБОИХ уравнениях получить одинаковое число либо х либо у (я так решаю всегда).
В твоем случае я домножила 5у на -2у, а 2у на 5у.
Получили -10у и 10у! Обязательно должно быть одно отрицательное и одно положительное, чтобы их можно было убрать. (в твоем случае).
Ну, а дальше думаю, ты поняла)

1)
ОДЗ: 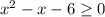 ⇒
⇒ 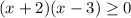 ⇒
⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
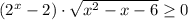 ⇔
⇔
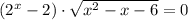 или
или 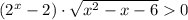
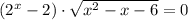 ⇒
⇒ 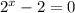 или
или 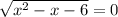 ⇒
⇒
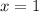 или
или  или
или 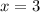
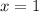 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 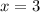
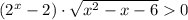 при
при ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
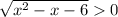 , тогда
, тогда 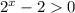 ⇒
⇒ 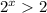 ⇒
⇒ 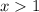
C учетом ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png) получаем ответ:
получаем ответ:
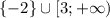
2)
ОДЗ: 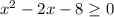 ⇒
⇒ 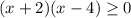 ⇒
⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
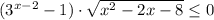 ⇔
⇔
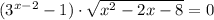 или
или 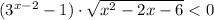
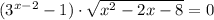 ⇒
⇒ 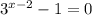 или
или 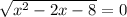 ⇒
⇒
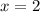 или
или  или
или 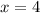
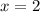 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 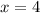
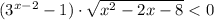 при
при ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
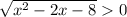 , тогда
, тогда 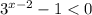 ⇒
⇒ 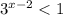 ⇒
⇒ 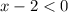
C учетом ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png) получаем ответ:
получаем ответ:
![(-\infty;-2]\cup \{2\}](/tpl/images/1361/5355/83f26.png)
3)
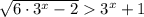
Так как 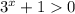 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
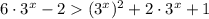
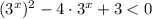
D=16-12=4
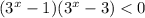
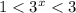
Показательная функция с основанием 3 возрастает
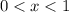
О т в е т. (0;1)
4)

Так как 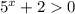 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
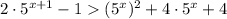
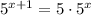
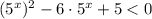
D=36-20=16
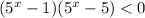
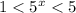
Показательная функция с основанием 5 возрастает
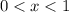
О т в е т. (0;1)
1)2,(3)
1.х=2,(3)
2.10х=23,(3)
3.из второго вычитаем первое => 9х=21
4.х=21/9=2, 1/3
2)1,(33)
1.х=1,(33)
2.100х=133,(33)
3.2-1 =>90х=132
4.132/90 = 1, 7/15
3)3,5(6)
1.х=3,5(6)
2.10х=35,(6)
3.100х=356,(6)
4.2-1 =>90х=321
5.321/90 = 3, 51/90
4)0,(66)
1.х=0,(66)
2.100х=66,(66)
3.99х=66
4.66/99 = 6/9