Задача. При каких значениях параметра 
система
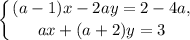
имеет бесконечное множество решений?
Решение. Система линейных уравнений, которая имеет вид
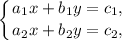
допускает три варианта решений:
1. Имеет одно решение:
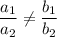
2. Не имеет решений:
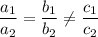
3. Имеет бесконечное количество решений:
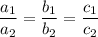
Таким образом, заданная система линейных уравнений будет иметь бесконечное количество решений, если:
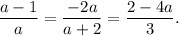
Следовательно, нужно рассмотреть три пары уравнений, из которых нужно выбрать корень (корни), который встречается у всех трех уравнений:
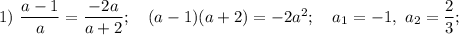
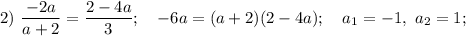
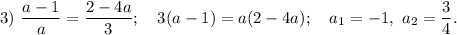
Значит, при 
все три выражения равны друг другу, откуда делаем вывод, что данная система будет иметь бесконечное количество решений.
ответ: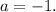 
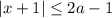
Рассмотрим 3 случая: с отрицательной, нулевой и положительной правой частью.
1. Если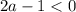 
, то есть 
.
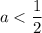Тогда предполагается, что модуль должен принимать значения, не большие некоторого отрицательного, то есть тоже отрицательные. Но модуль не может принимать отрицательных значений. Значит, в этом случае неравенство решений не имеет.
2. Если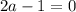 
, то есть 
.
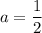Получаем неравенство:
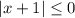
Поскольку модуль не принимает отрицательных значений, достаточно решить уравнение:
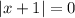
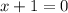
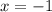
3. Если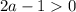 
, то есть 
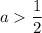, то получаем неравенство с положительной правой частью:
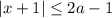
Заменим его следующим двойным неравенством:
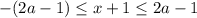
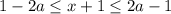
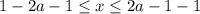
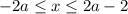
Таким образом получаем ответ:
при 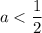: решений нет
при :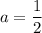
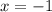
при 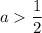: ![x\in[-2a;\ 2a-2]](/tpl/images/2004/6663/9d563.png)
1,0303...; 0,666666; -3,242424; 2,010010001;