1
Здесь заметим, что первый из углов - это 2π или π/2. Значит, воспользуемся формулами приведения:
ctg(2п+a)*sin(п\2+a) / (cos(п-a)*tg(3п\2-a) = ctg a * cos a / -cos a * ctg a = cos a / -cos a = -1
2
Cначала преобразуем числитель отдельно. Для его преобразований воспользуемся формулами двойного аргумента.
16sin12º*cos12º*cos24º = 8 * 2sin12º*cos12º*cos24º = 8sin 24°cos 24° = 4 * 2sin 24°cos 24° = 4sin 48°
Получим,
4sin 48° / cos 42° = 4sin(90° - 42°) / cos 42° = 4cos 42° / cos 42° = 4
3
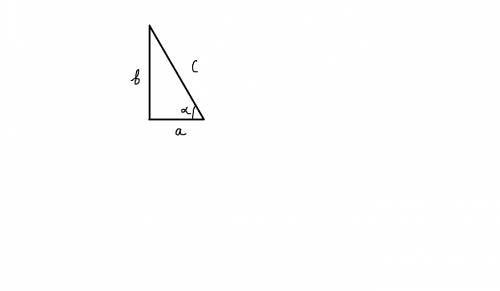
Здесь вся сложность заключается в том, чтобы найти точное значение выражения ctg(arccos 1/4). Поэтому для его нахождения воспользуемся методом прямоугольного треугольника(рисунок сейчас приложу). Рассмотрим прямоугольный треугольник.
Пусть arccos 1/4 = α, тогда по определению арккосинуса cosα = 1/4
По сути, как несложно догадаться, нам нужно найти ctg α, зная его косинус.
cos α = a/c
a/c = 1/4, отсюда a = 1, c = 4
ctg α = a/b, не хватает только лишь b. Найдём её по теореме Пифагора,
b² = c² - a²
b² = 16 - 1 = 15
b = √15
Тогда, ctg α = a/b = 1/√15 = √15/15
Но α = arccos 1/4. Значит, ctg(arccos 1/4) = √15/15
Теперь осталось только верно посчитать:
2⁻² = 1/4
√15 / 15 - 1/4 = (2√15 - 15 )/ 60
Решите квадратные уравнения и неравенства: 1)2(3+5x)<3(7x-4)-4
6+10x<21x-12-4
10x-21x<-12-4-6
-11x=-22
x=2
2.)(x-1)2-5≤(x+4)2
2x-2-5≤2x+8
2x-2x≤15 не имеет значения .
Решите линейные уравнения и неравенства:
1.)3х+5=3х-1
3x-3x=-5-1-не имеет значения
2.)2-3(х+2)=5-2х
2-3x-6=5-2x
-3x+2x=5-2
-x=3 /(-1)
x=-3
3.)4х-5.5=5х-3(2х-1.5)
4x-5.5=5x-6x+4.5
4x-5x+6x=5.5+4.5
5x=10
x=2
4.)2(3+5х)<3(7х-4)-4;
6+10x<21x-12-4
10x-21x<-12-4-6
-11x=-22
x=2
5.)(x-1)2-5≤(x+4)2
2x-2-5≤2x+8
2x-2x≤15 не имеет значения .
х км/ч - скорость лодки
х+2 км/ч - скорость по течению
х-2 км/ч - скорость против течения
6/(х-2) ч - время в пути против течения
8/(х+2) ч - время в пути по течению.
Всего в пути - 1 час.
.
6/(х-2) +8/(х+2)=1
6(х+2)+8(х-2)=(х+2)(х-2)
6х+12+8х-16=х² - 4
14х-4=х²-4
х²-14х=0
х(х-14)=0
х1=0 - не подходит решению
х-14=0
х2=14(км/ч) - скорость лодки