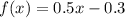1. Прямоугольник - это параллелограмм, у которого все углы прямые.
2. Диагонали прямоугольника равны. Пусть ABCD - прямоугольник. В нем проведены диагонали AC и BD. Рассмотрим ΔBAD и ΔCDA. В них: 1. ∠BAD = ∠CDA = 90 2. AB = CD (как противолежащие стороны параллелограмма) 3. AD - общий катет Получаем, что ΔBAD = ΔCDA по 2 сторонам и углу между ними. Отсюда следует, что гипотенузы этих треугольников тоже равны. А т.к. гипотенузы и есть диагонали прямоугольника, то получили AC = BD. Что и требовалось доказать
Искомая функция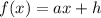
.
Найдем значения искомой функции в заданных точках х:
Кроме этого, для каждого из аргументов есть еще и экспериментальное значение, которое обозначим через функцию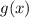
:
Составим функцию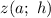
, которая будет суммировать квадраты разностей значений функций 
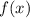и 
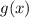соответствующих аргументов:
Исследуем эту функцию на экстремум.
Найдем частные производные:
Необходимое условие экстремума: равенство нулю частных производных:
Домножим второе уравнение на (-3):
Складываем уравнения:
Подставим значение а во второе уравнение исходной системы:
Точка (0.5; -0.3) - предполагаемая точка экстремума.
Найдем вторые частные производные функции:
Рассмотрим выражение:
Так как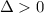
и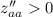 
, то точка (0.5; -0.3) является точкой минимума.
Значит, в точке (0.5; -0.3) функция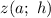
имеет минимум.
Тогда, значения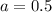
и 
есть искомые коэффициенты функции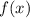 
.
ответ: