1) Если функция f(x) задана графиком, то нужно найти на графике координату у₀ вершины параболы.
Если ветви параболы направлены вниз, то область значений E(f)=(-∞;y₀].
Если ветви параболы направлены вверх, то область значений E(f)=[y₀;+∞).
------------------------------------------------------------------------
2) Если функция задана формулой f(x) = ax²+bx+c, то сначала нужно найти координаты вершины. Сначала координату х :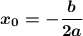 
. Затем ее подставить в формулу и найти координату у₀=f(x₀)=ax₀²+bx₀+c.
Если a>0, то область значений функции E(f)=[y₀;+∞).
Если а<0, то область значений функции E(f)=(-∞;y₀].
----------------------------------------------------------------------------------
3) Если функция задана формулой вида f(x) = a(x - x₀)² + у₀, то координаты вершины параболы присутствуют в явном виде (x₀; y₀).
Если a>0, то область значений функции E(f)=[y₀;+∞).
Если а<0, то область значений функции E(f)=(-∞;y₀].
f`(x)=(4-2x)`=(4)`-(2x)`=0-2·(x)`=-2·1=-2
Применили правила:
производная суммы( разности) равна сумме( разности) производных
Производная постоянной (C)`=0
Постоянный множитель можно вынести за знак производной
(х)`=1
Производная принимает во всех точках одно и то же значение (-2)
f`(0,5)=f`(-3)=-2
в) f(x)=3x-2
f`(x)=(3x-2)`=(3х)`-(2)`=3·(x)`-0=3·1=3
Применили правила:
производная суммы( разности) равна сумме( разности) производных
Производная постоянной (C)`=0
Постоянный множитель можно вынести за знак производной
(х)`=1
Производная принимает во всех точках одно и то же значение (3)
f`(5)=f`(-2)=3