Испытание состоит в том, что два раза подряд бросают игральный кубик.
Число исходов испытания
n=6·6=36
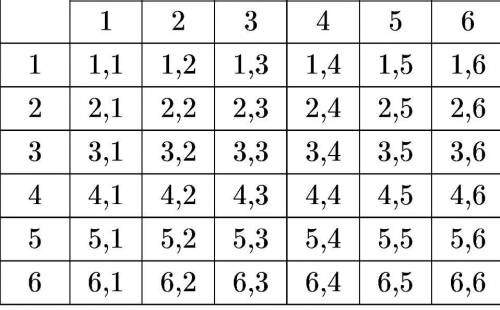
Результаты можно изобразить в виде таблицы:
( см. рис.1)
Первая цифра -число очков, выпавшее на первом кубике,
вторая цифра - число очков, выпавшее на первом кубике.
Получаем 36 двузначных чисел:
от 11 до 16; от 21 до 26; ... от 61 до 66.
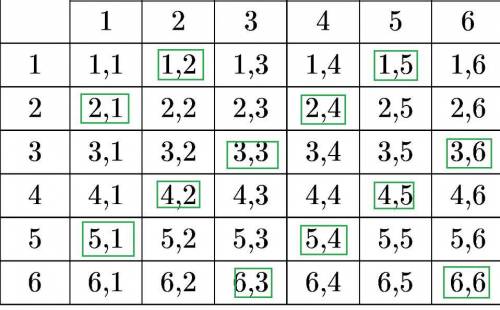
Событие A-"результатом двух последовательных бросков игрального кубика будет число, кратное трем"
m=12 ( cм. рис. 2)
это двузначные числа:
12;15; 21;24;33;36;42;45;51;54;63;66
По формуле классической вероятности
p(A)=m/n=12/36=1/3
1) В коробке находятся 5 красных, 6 зеленых и 4 розовых карандаша. Найдите вероятность того, что вытащат красный карандаш
Решение: 5/15 = 0,33
2) В коробке лежат 3 красных, 4 синий и 5 зеленых шаров. Определить вероятность вытаскивания красного шарика.
Решение: 3/12 = 0,25
3)В коробке лежат 7 красных, 6 синих и 5 зеленых карандашей. Какое наибольшее число желтых карандашей можно положить в эту коробку, чтобы вероятность наугад достать из коробки синий шарик была не меньше 0,3
x/18 = 3/10;
x = 18*3/10 = 5,4т.е. 5 штук
Объяснение:
решение
Объяснение:
(
4
x
−
3
)
2
+
(
2
x
−
1
)
(
2
x
+
1
)
−
2
=
0
Упрощение
(
4
x
−
3
)
2
+
(
2
x
−
1
)
(
2
x
+
1
)
−
2
(
4
x
−
3
)
2
+
(
2
x
−
1
)
(
2
x
+
1
)
−
2
=
Раскрытие скобок:
8
x
−
6
+
4
x
2
+
2
x
−
2
x
−
1
−
2
=
8
x
−
9
+
4
x
2
=
4
x
2
+
8
x
−
9
4
x
2
+
8
x
−
9
4
x
2
+
8
x
−
9
=
0
Вычислим дискриминант.
D
=
b
2
−
4
a
c
=
208
x
1
,
2
=
−
b
±
√
D
2
a
=
−
8
±
√
208
8
=
−
8
±
4
√
13
8
x
1
=
−
2
+
√
13
2
≈
0,802
8
,
x
2
=
−
2
−
√
13
2
≈
−
2,802
8